Question

Let $f(x) = \left(sin\frac{kx}{10}\right)^4 + \left(cos\frac{kx}{10}\right)^4$, $k \in N$

If $\{f(x):a<x<a+1\} = \{f(x):x \in R\}$ for any real number a then the minimum value of k is more than

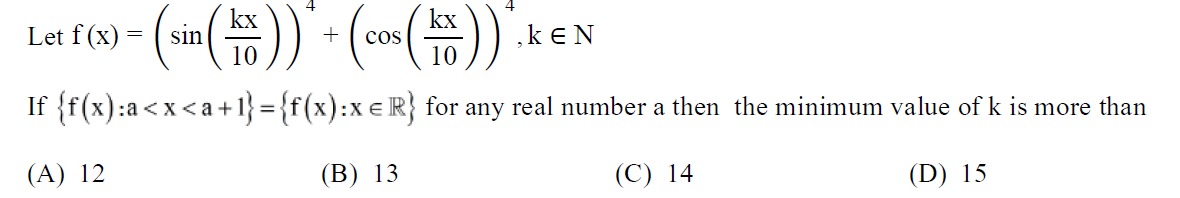
• A. 12
• B. 13
• C. 14
• D. 15

Answer 1

Answer: (D)

D

Answer 2

The given function is $f(x) = \left(\sin\frac{kx}{10}\right)^4 + \left(\cos\frac{kx}{10}\right)^4$. We can simplify this expression: $f(x) = (\sin^2\frac{kx}{10} + \cos^2\frac{kx}{10})^2 - 2\sin^2\frac{kx}{10}\cos^2\frac{kx}{10}$ $f(x) = 1 - \frac{1}{2}\left(2\sin\frac{kx}{10}\cos\frac{kx}{10}\right)^2$ $f(x) = 1 - \frac{1}{2}\left(\sin\left(2 \cdot \frac{kx}{10}\right)\right)^2$ $f(x) = 1 - \frac{1}{2}\sin^2\left(\frac{kx}{5}\right)$

Let $\theta = \frac{kx}{5}$. The function becomes $f(x) = 1 - \frac{1}{2}\sin^2(\theta)$. The range of $\sin^2(\theta)$ is $[0, 1]$. So, the range of $\frac{1}{2}\sin^2(\theta)$ is $\left[0, \frac{1}{2}\right]$. Multiplying by -1, the range of $-\frac{1}{2}\sin^2(\theta)$ is $\left[-\frac{1}{2}, 0\right]$. Adding 1, the range of $f(x)$ is $\left[1 - \frac{1}{2}, 1 - 0\right] = \left[\frac{1}{2}, 1\right]$. This is the range of $f(x)$ for $x \in R$, i.e., $\{f(x):x \in R\} = \left[\frac{1}{2}, 1\right]$.

The condition given is that $\{f(x):a<x<a+1\} = \{f(x):x \in R\}$ for any real number $a$. This means that on any interval of length 1, the function $f(x)$ must attain all values between $\frac{1}{2}$ and $1$.

Let's find the period of $f(x)$. The term $\sin^2\left(\frac{kx}{5}\right)$ determines the periodicity. The period of $\sin(Ax)$ is $\frac{2\pi}{|A|}$. The period of $\sin^2(Ax)$ is $\frac{\pi}{|A|}$. Here $A = \frac{k}{5}$. So, the period of $f(x)$ is $T = \frac{\pi}{|k/5|} = \frac{5\pi}{k}$ (since $k \in N$, $k>0$).

For a periodic function to cover its entire range on any interval of length $L$, it is necessary that $L \ge T$. In this problem, the length of the interval is $L=1$. Therefore, we must have $1 \ge T$. $1 \ge \frac{5\pi}{k}$ Since $k \in N$, $k$ must be positive, so we can multiply by $k$ without changing the inequality direction: $k \ge 5\pi$

Now, we need to approximate the value of $5\pi$. Using $\pi \approx 3.14159$: $5\pi \approx 5 \times 3.14159 = 15.70795$

So, $k \ge 15.70795$. Since $k$ must be a natural number ($k \in N$), the minimum integer value of $k$ that satisfies this condition is $k=16$.

The question asks for "the minimum value of k is more than". The minimum value of $k$ is 16. We need to find which of the given options (A) 12, (B) 13, (C) 14, (D) 15 is a value that 16 is greater than. In this case, 15 is the largest value among the options that 16 is greater than.