Question
Question: Let $f(x) = \int \frac{\sin x + \cos x}{e^{-x} + \sin x} dx$ and $f(0)=1$, then $f(x)$ is equal to:...
Let f(x)=∫e−x+sinxsinx+cosxdx and f(0)=1, then f(x) is equal to:
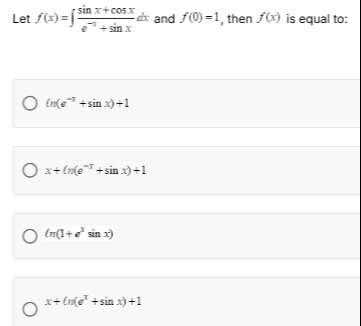
ln(e−x+sinx)+1
x+ln(e−x+sinx)+1
ln(1+exsinx)
x+ln(ex+sinx)+1
x+ln(e^{-x}+sin x)+1
Solution
To evaluate the integral f(x)=∫e−x+sinxsinx+cosxdx, we can manipulate the integrand.
The denominator is e−x+sinx. We can rewrite e−x as ex1. So, the denominator becomes ex1+sinx=ex1+exsinx.
Substitute this back into the integral: f(x)=∫ex1+exsinxsinx+cosxdx f(x)=∫1+exsinxex(sinx+cosx)dx
Now, this integral is in the form ∫g(x)g′(x)dx. Let g(x)=1+exsinx. To find g′(x), we differentiate g(x) with respect to x: g′(x)=dxd(1+exsinx) Using the product rule for exsinx: dxd(uv)=u′v+uv′. Here, u=ex and v=sinx. So u′=ex and v′=cosx. g′(x)=0+(exsinx+excosx) g′(x)=ex(sinx+cosx)
We can see that the numerator of our manipulated integrand is exactly g′(x). So, the integral becomes: f(x)=∫g(x)g′(x)dx=ln∣g(x)∣+C Substitute back g(x)=1+exsinx: f(x)=ln∣1+exsinx∣+C
Now, we use the given condition f(0)=1 to find the value of C. f(0)=ln∣1+e0sin0∣+C Since e0=1 and sin0=0: f(0)=ln∣1+1⋅0∣+C f(0)=ln∣1∣+C f(0)=0+C Given f(0)=1, so C=1.
Thus, the function f(x) is: f(x)=ln∣1+exsinx∣+1
Now, let's compare this result with the given options. Notice that the options do not have absolute values. We should match the algebraic form. Let's look at Option 2: x+ln(e−x+sinx)+1. Let's simplify the logarithmic term in Option 2: ln(e−x+sinx)=ln(ex1+sinx) =ln(ex1+exsinx) Using the logarithm property ln(BA)=lnA−lnB: =ln(1+exsinx)−ln(ex) =ln(1+exsinx)−x Substitute this back into Option 2: f(x)=x+(ln(1+exsinx)−x)+1 f(x)=ln(1+exsinx)+1 This matches our derived function f(x), ignoring the absolute value sign which is common in multiple-choice questions when the domain is implicitly assumed to make the argument of logarithm positive.
The final answer is x+ln(e−x+sinx)+1.
