Question

Let $f(x) = \int \frac{dx}{(3+4x^2)\sqrt{4-3x^2}}$, $|x| < \frac{2}{\sqrt{3}}$. If $f(0) = 0$ and $f(1) = \frac{1}{\alpha\beta} \tan^{-1}(\frac{\alpha}{\beta})$, $\alpha, \beta > 0$, then $\alpha^2 + \beta^2$ is equal to

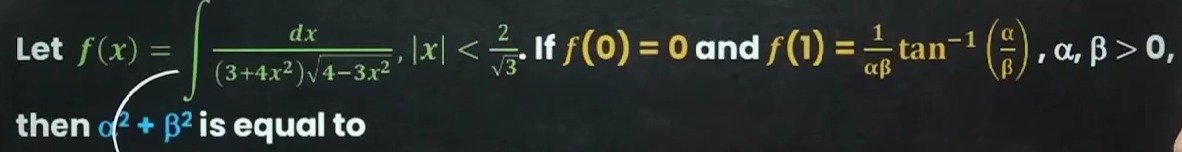
• A. 28
• B. 25
• C. 3
• D. 5

Answer 1

Answer: (A)

28

Answer 2

The integral is solved using the substitution $x = \frac{2}{\sqrt{3}} \sin \theta$. This transforms the integrand into a form involving $\sin^2\theta$, which is then converted to an integral in $\tan\theta$. The resulting integral is a standard arctangent form. After expressing the result in terms of $x$ and using the initial condition $f(0)=0$ to find the constant of integration, the value of $f(1)$ is computed. Comparing this with the given form of $f(1)$, the values of $\alpha$ and $\beta$ are determined, and finally $\alpha^2 + \beta^2$ is calculated to be 28.