Question
Question: Let $f(x) = cos^{-1}(2x\sqrt{1-x^2})$ then $f'(\frac{\sqrt{3}}{2})$ equals...
Let f(x)=cos−1(2x1−x2) then f′(23) equals
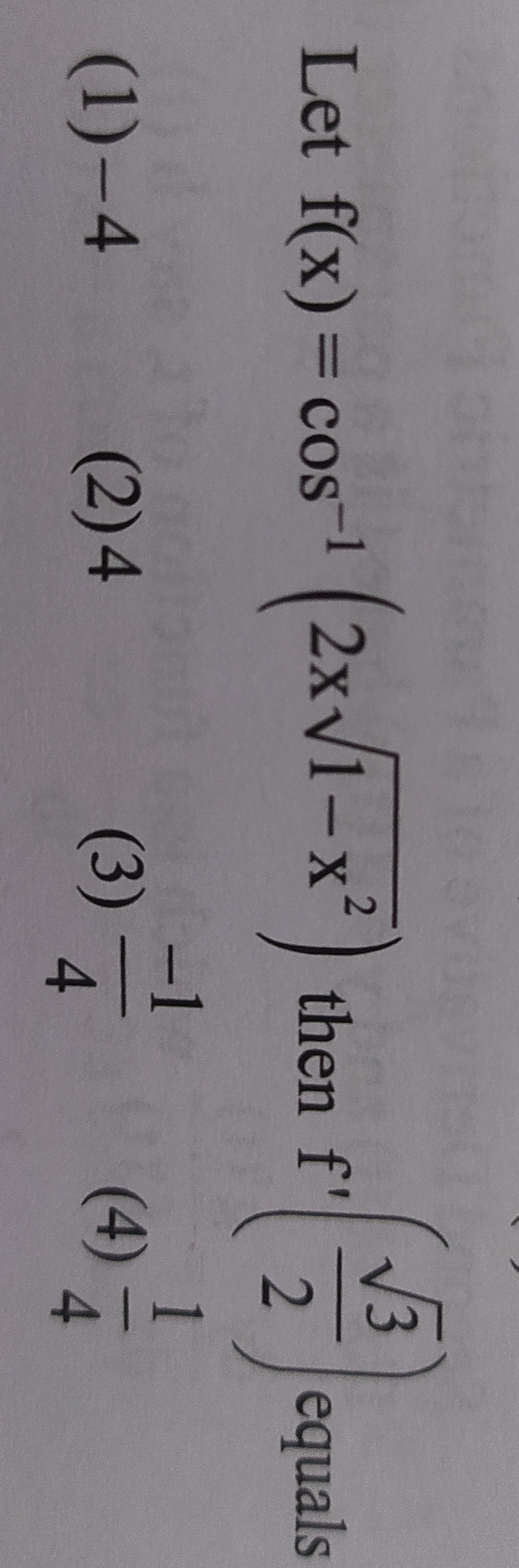
-4
4
4−1
41
4
Solution
To find f′(23) for f(x)=cos−1(2x1−x2), we can use two methods:
Method 1: Using Trigonometric Substitution
Let x=sinθ. Since x=23 is positive, we can choose θ∈[0,2π]. Then 1−x2=1−sin2θ=cos2θ=cosθ (since cosθ≥0 for θ∈[0,2π]).
Substitute x=sinθ into f(x): f(x)=cos−1(2sinθcosθ) f(x)=cos−1(sin(2θ))
Now, use the identity sinA=cos(2π−A): f(x)=cos−1(cos(2π−2θ))
For x=23, we have sinθ=23, which implies θ=3π. Then 2θ=32π. So, 2π−2θ=2π−32π=63π−4π=−6π.
Now, we have f(x)=cos−1(cos(−6π)). The principal value branch of cos−1(y) is [0,π]. Since −6π is not in [0,π], we use the property cos−1(cosA)=−A if A∈[−π,0]. Here A=−6π, which is in [−π,0]. So, f(x)=−(−6π)=6π. This is the value of the function at x=23, not the derivative.
To find the derivative, we need the functional form of f(x) for the relevant range of x. For x=23, θ=3π. The angle 2π−2θ=−6π falls in the range [−2π,0). For A∈[−2π,0), cos−1(cosA)=−A. So, f(x)=−(2π−2θ)=2θ−2π. Substitute back θ=sin−1x: f(x)=2sin−1x−2π.
Now, differentiate f(x) with respect to x: f′(x)=dxd(2sin−1x−2π) f′(x)=2⋅1−x21−0 f′(x)=1−x22
Finally, substitute x=23: f′(23)=1−(23)22=1−432=412=212=4.
Method 2: Direct Differentiation using Chain Rule
Let f(x)=cos−1(2x1−x2). Using the chain rule, dxdcos−1(u)=1−u2−1dxdu. Here, u=2x1−x2.
First, find dxdu using the product rule: u=2x(1−x2)1/2 dxdu=2[(1)⋅(1−x2)1/2+x⋅21(1−x2)−1/2(−2x)] dxdu=2[1−x2−1−x2x2] dxdu=2[1−x2(1−x2)−x2]=1−x22(1−2x2).
Now, evaluate dxdu at x=23: dxdux=23=1−(23)22(1−2(23)2)=1−432(1−2⋅43)=412(1−23)=212(−21)=21−1=−2.
Next, evaluate u at x=23: u=2(23)1−(23)2=31−43=341=3⋅21=23.
Finally, evaluate 1−u2 at x=23 (where u=23): 1−u2=1−(23)2=1−43=41=21.
Now, substitute these values into the derivative formula f′(x)=1−u2−1⋅dxdu: f′(23)=21−1⋅(−2)=(−2)⋅(−2)=4.
Both methods yield the same result.
