Question

Let $f(x)$ be an even quadratic polynomial such that $-4 \le f(1) \le -1$ & $-1 \le f(2) \le 5$. Which of the following statements is true ?

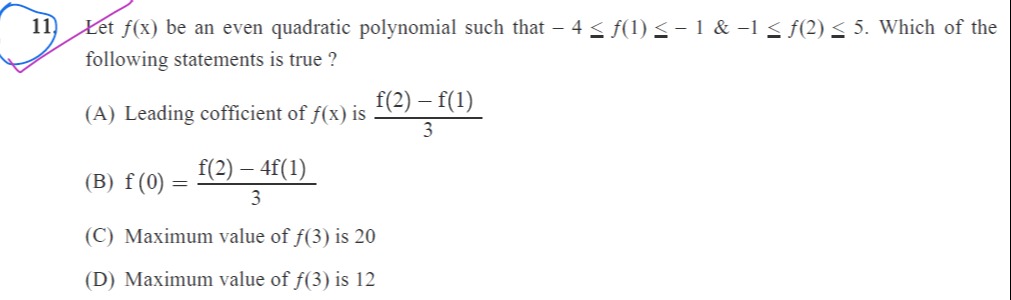
• A. Leading cofficient of $f(x)$ is $\frac{f(2)-f(1)}{3}$
• B. $f(0) = \frac{f(2)-4f(1)}{3}$
• C. Maximum value of $f(3)$ is 20
• D. Maximum value of $f(3)$ is 12

Answer 1

Answer: (A), (C)

(A) and (C)

Answer 2

We are given that $f(x)$ is an even quadratic polynomial, so it can be written as $f(x) = ax^2 + c$. Then, we have:

$f(1) = a + c$ $f(2) = 4a + c$

Step 1: Analyzing Option A

Subtracting the first equation from the second gives:

$f(2) - f(1) = (4a + c) - (a + c) = 3a$

Therefore, $a = \frac{f(2) - f(1)}{3}$. Thus, option (A) is correct.

Step 2: Analyzing Option B

We know that $c = f(0)$. Also, we can express $c$ as:

$c = f(1) - a = f(1) - \frac{f(2) - f(1)}{3} = \frac{3f(1) - (f(2) - f(1))}{3} = \frac{4f(1) - f(2)}{3}$

Option (B) states that $f(0) = \frac{f(2) - 4f(1)}{3}$, which is the negative of our result. So, option (B) is false.

Step 3: Analyzing Options C and D (Maximum value of $f(3)$)

We have $f(3) = 9a + c$. Substituting the expressions for $a$ and $c$ we found earlier:

$f(3) = 9\left(\frac{f(2) - f(1)}{3}\right) + \frac{4f(1) - f(2)}{3} = 3(f(2) - f(1)) + \frac{4f(1) - f(2)}{3}$

Writing with a common denominator:

$f(3) = \frac{9(f(2) - f(1)) + 4f(1) - f(2)}{3} = \frac{8f(2) - 5f(1)}{3}$

Given $-4 \le f(1) \le -1$ and $-1 \le f(2) \le 5$, the expression $\frac{8f(2) - 5f(1)}{3}$ is maximized when $f(2)$ is as large as possible and $f(1)$ is as small as possible. That is, we choose:

$f(2) = 5$, $f(1) = -4$

Then,

$f(3) = \frac{8(5) - 5(-4)}{3} = \frac{40 + 20}{3} = \frac{60}{3} = 20$

Thus, the maximum of $f(3)$ is $20$, and option (C) is correct, while option (D) is false.

Therefore, the correct options are (A) and (C).