Question
Question: Let f(x) be a twice differentiable function such that f''(0) = 2, then the value of $\lim_{x\to 0} \...
Let f(x) be a twice differentiable function such that f''(0) = 2, then the value of limx→0x2f(5x)−3f(3x)+2f(2x)
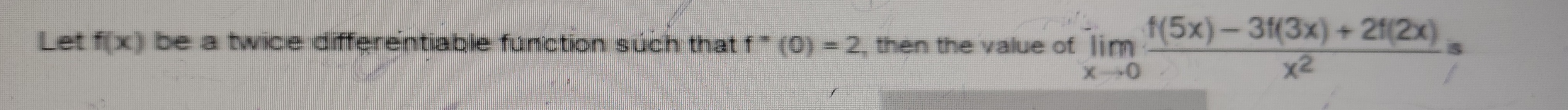
6
Solution
The limit is of the indeterminate form 00. Applying L'Hopital's rule twice, we differentiate the numerator and the denominator twice.
The first differentiation of the numerator yields 5f′(5x)−9f′(3x)+4f′(2x), and the denominator becomes 2x. This is still 00 at x=0.
The second differentiation of the numerator yields 25f′′(5x)−27f′′(3x)+8f′′(2x), and the denominator becomes 2. Evaluating the limit as x→0, we get 225f′′(0)−27f′′(0)+8f′′(0)=26f′′(0)=3f′′(0). Given f′′(0)=2, the limit is 3×2=6.
Alternatively, using the Taylor expansion of f(x) around x=0 up to the second order term, f(x)=f(0)+f′(0)x+2f′′(0)x2+O(x3). Substituting 5x, 3x, and 2x into this expansion and combining the terms in the numerator, we find that the numerator is equal to 3f′′(0)x2+O(x3). Dividing by x2 and taking the limit as x→0, we get 3f′′(0), which evaluates to 3×2=6.
