Question

Let $f(x)$ be a real polynomial of least degree which has local minimum at $x=1$ and local maximum at $x=-\frac{1}{3}$ and $f(2)=0, f(3)=13$, then value of $f(6)$ is _______.

Answer 1

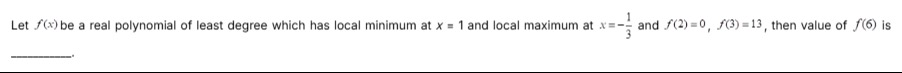
172

Answer 2

To find the polynomial $f(x)$, we use the given information about its local extrema and function values.

1. Determine the degree of the polynomial:
   A polynomial has local extrema where its derivative $f'(x)=0$. We are given that $f(x)$ has a local minimum at $x=1$ and a local maximum at $x=-\frac{1}{3}$. This means $f'(1)=0$ and $f'\left(-\frac{1}{3}\right)=0$.
   Since $f'(x)$ has two distinct roots, $x=1$ and $x=-\frac{1}{3}$, the least degree of $f'(x)$ must be 2.
   If $f'(x)$ is a quadratic polynomial, then $f(x)$ must be a cubic polynomial. This is the polynomial of least degree satisfying the conditions.

2. Formulate $f'(x)$:
   Since $x=1$ and $x=-\frac{1}{3}$ are roots of $f'(x)$, we can write $f'(x)$ in the form:
   $f'(x) = A(x-1)\left(x+\frac{1}{3}\right)$
   where $A$ is a constant.
   Expand $f'(x)$:
   $f'(x) = A\left(x^2 + \frac{1}{3}x - x - \frac{1}{3}\right)$
   $f'(x) = A\left(x^2 - \frac{2}{3}x - \frac{1}{3}\right)$

3. Integrate $f'(x)$ to find $f(x)$:
   Integrate $f'(x)$ with respect to $x$:
   $f(x) = \int A\left(x^2 - \frac{2}{3}x - \frac{1}{3}\right) dx$
   $f(x) = A\left(\frac{x^3}{3} - \frac{2}{3}\cdot\frac{x^2}{2} - \frac{1}{3}x\right) + C$
   $f(x) = A\left(\frac{x^3}{3} - \frac{x^2}{3} - \frac{x}{3}\right) + C$
   We can factor out $\frac{A}{3}$:
   $f(x) = \frac{A}{3}(x^3 - x^2 - x) + C$

4. Use the given conditions to find constants A and C:
   We are given $f(2)=0$ and $f(3)=13$.
   Using $f(2)=0$:
   $\frac{A}{3}(2^3 - 2^2 - 2) + C = 0$
   $\frac{A}{3}(8 - 4 - 2) + C = 0$
   $\frac{A}{3}(2) + C = 0$
   $\frac{2A}{3} + C = 0 \quad (1)$

   Using $f(3)=13$:
   $\frac{A}{3}(3^3 - 3^2 - 3) + C = 13$
   $\frac{A}{3}(27 - 9 - 3) + C = 13$
   $\frac{A}{3}(15) + C = 13$
   $5A + C = 13 \quad (2)$

   Now, solve the system of equations (1) and (2).
   From (1), $C = -\frac{2A}{3}$.
   Substitute this into (2):
   $5A - \frac{2A}{3} = 13$
   Multiply by 3 to clear the denominator:
   $15A - 2A = 39$
   $13A = 39$
   $A = 3$

   Now substitute $A=3$ back into the expression for $C$:
   $C = -\frac{2(3)}{3} = -2$

5. Write the complete polynomial $f(x)$:
   Substitute $A=3$ and $C=-2$ into the expression for $f(x)$:
   $f(x) = \frac{3}{3}(x^3 - x^2 - x) - 2$
   $f(x) = x^3 - x^2 - x - 2$

6. Verify local extrema (optional but good practice):
   $f'(x) = 3x^2 - 2x - 1 = (3x+1)(x-1)$. Roots are $x=1$ and $x=-\frac{1}{3}$.
   $f''(x) = 6x - 2$.
   $f''(1) = 6(1) - 2 = 4 > 0$, so $x=1$ is a local minimum.
   $f''\left(-\frac{1}{3}\right) = 6\left(-\frac{1}{3}\right) - 2 = -2 - 2 = -4 < 0$, so $x=-\frac{1}{3}$ is a local maximum.
   The polynomial satisfies all conditions.

7. Calculate $f(6)$:
   Substitute $x=6$ into $f(x)$:
   $f(6) = (6)^3 - (6)^2 - (6) - 2$
   $f(6) = 216 - 36 - 6 - 2$
   $f(6) = 180 - 6 - 2$
   $f(6) = 174 - 2$
   $f(6) = 172$