Question

Let f(x) be a differentiable function satisfying $f'(x) \leq 2 - f(x)$, $\forall x \in R$, f(0) = 0. If the maximum value of f(2) is M, then [M] is (where [.] denotes greatest integer function)

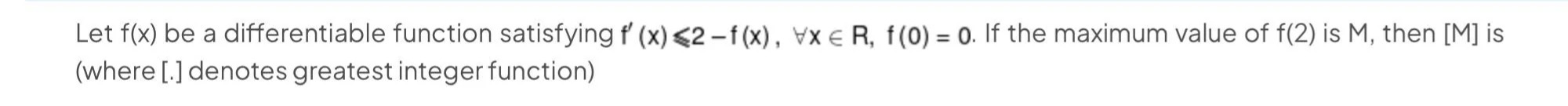
Answer 1

1

Answer 2

Solution Explanation:
We are given

$$f'(x) \le 2 - f(x), \quad f(0)=0.$$

Consider the equality case:

$$g'(x) = 2 - g(x), \quad g(0)=0.$$

This is a linear differential equation. Rearranging,

$$g'(x) + g(x) = 2.$$

The integrating factor is $e^x$. Multiplying through by $e^x$,

$$\frac{d}{dx}[e^x g(x)] = 2e^x.$$

Integrate from 0 to $x$:

$$e^x g(x) - e^0 g(0) = 2(e^x - 1).$$

Since $g(0)=0$,

$$e^x g(x)=2(e^x-1) \quad \Rightarrow \quad g(x) = 2\left(1-\frac{1}{e^x}\right)=2-2e^{-x}.$$

Since $f'(x) \leq 2-f(x)$, by the comparison principle, for all $x$,

$$f(x) \leq g(x)=2-2e^{-x}.$$

Thus, the maximum possible $f(2)$ is

$$f(2)\leq 2-2e^{-2}.$$

Evaluating, $M=2-2e^{-2}$. Note that numerically, $e^{-2}\approx0.1353$ so $M\approx2-0.2706=1.7294$. The greatest integer function $[M]$ is therefore

$$[M]=1.$$