Question

Let f(x) be a cubic polynomial which has local maximum at x=-1 and f'(x) has a local minimum at x = 1. If f(-1)=10 and f(3)=-22, if the distance between its two horizontal tangents is D then $\frac{D}{8}$ is ______.

Answer 1

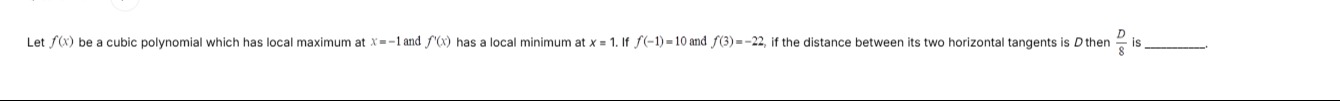
4

Answer 2

Let the cubic polynomial be $f(x) = ax^3 + bx^2 + cx + d$. The first derivative is $f'(x) = 3ax^2 + 2bx + c$. The second derivative is $f''(x) = 6ax + 2b$.

We are given that $f(x)$ has a local maximum at $x = -1$. This implies $f'(-1) = 0$. We are also given that $f'(x)$ has a local minimum at $x = 1$. This implies $f''(1) = 0$.

From $f''(1) = 0$: $6a(1) + 2b = 0 \implies 6a + 2b = 0 \implies b = -3a$.

From $f'(-1) = 0$: $3a(-1)^2 + 2b(-1) + c = 0$ $3a - 2b + c = 0$. Substitute $b = -3a$: $3a - 2(-3a) + c = 0$ $3a + 6a + c = 0$ $9a + c = 0 \implies c = -9a$.

So, $f(x) = ax^3 - 3ax^2 - 9ax + d$. And $f'(x) = 3ax^2 - 6ax - 9a = 3a(x^2 - 2x - 3)$.

The horizontal tangents occur where $f'(x) = 0$. $3a(x^2 - 2x - 3) = 0$. $x^2 - 2x - 3 = 0$. $(x-3)(x+1) = 0$. The x-coordinates of the horizontal tangents are $x = -1$ and $x = 3$.

The y-values of the horizontal tangents are $f(-1)$ and $f(3)$. We are given $f(-1) = 10$ and $f(3) = -22$. The distance between these two horizontal tangents is $D = |f(3) - f(-1)| = |-22 - 10| = |-32| = 32$.

The question asks for $\frac{D}{8}$. $\frac{D}{8} = \frac{32}{8} = 4$.