Question

Let $F(x)$ be a cubic polynomial defined by $F(x) = \frac{x^3}{3} + (a-3)x^2 + x - 13$, then the number of all possible integral values of $a$ in the interval $[1, 100]$ for which $F(x)$ has point of local minimum at $(\alpha, \beta)$, where $\alpha < 0$, is equal to

Answer 1

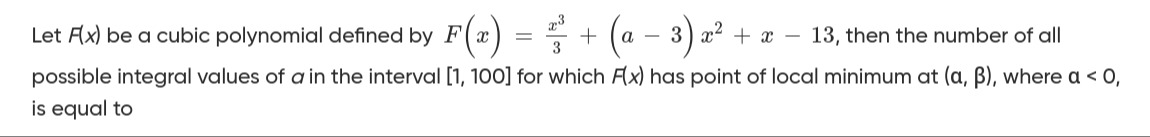
96

Answer 2

1. Find derivatives: $F'(x) = x^2 + 2(a-3)x + 1$ $F''(x) = 2x + 2(a-3)$

2. Find critical points: Set $F'(x) = 0 \implies x^2 + 2(a-3)x + 1 = 0$. The roots are $x = -(a-3) \pm \sqrt{(a-3)^2 - 1}$. For distinct real roots (required for local extrema), the discriminant must be positive: $(a-3)^2 - 1 > 0 \implies |a-3| > 1$, so $a > 4$ or $a < 2$.

3. Identify local minimum: Using the second derivative test, a local minimum occurs where $F''(x) > 0$. The roots are $x_1 = -(a-3) - \sqrt{(a-3)^2 - 1}$ and $x_2 = -(a-3) + \sqrt{(a-3)^2 - 1}$. $F''(x_1) = 2x_1 + 2(a-3) = -2\sqrt{(a-3)^2 - 1} < 0$ (local maximum). $F''(x_2) = 2x_2 + 2(a-3) = 2\sqrt{(a-3)^2 - 1} > 0$ (local minimum). So, the point of local minimum is $\alpha = x_2 = -(a-3) + \sqrt{(a-3)^2 - 1}$.

4. Apply condition $\alpha < 0$: $-(a-3) + \sqrt{(a-3)^2 - 1} < 0$ $\sqrt{(a-3)^2 - 1} < (a-3)$ Let $k = a-3$. Then $\sqrt{k^2 - 1} < k$. For this to hold, we need $k^2 - 1 \ge 0$ and $k > 0$. $k^2 \ge 1 \implies k \ge 1$ or $k \le -1$. Combined with $k > 0$, we get $k \ge 1$. Substituting back $k = a-3$, we have $a-3 \ge 1 \implies a \ge 4$.

5. Combine conditions on $a$: For a local minimum to exist: $a > 4$ or $a < 2$. For the local minimum to be at $\alpha < 0$: $a \ge 4$. The intersection is $a > 4$. (Note: $a=4$ leads to $D=0$, an inflection point, not a local minimum, so $a>4$ is strict).

6. Count integral values: We need to count integers $a$ in $[1, 100]$ such that $a > 4$. These are $5, 6, \dots, 100$. The number of values is $100 - 5 + 1 = 96$.