Question

Let f(x) = ax (a > 0) be written as f(x) = f1(x) + f2(x), where f1(x) is an even function and f2(x) is an odd function. Then f1(x + y) + f1(x - y) equals : [JEE(Main)-2019]

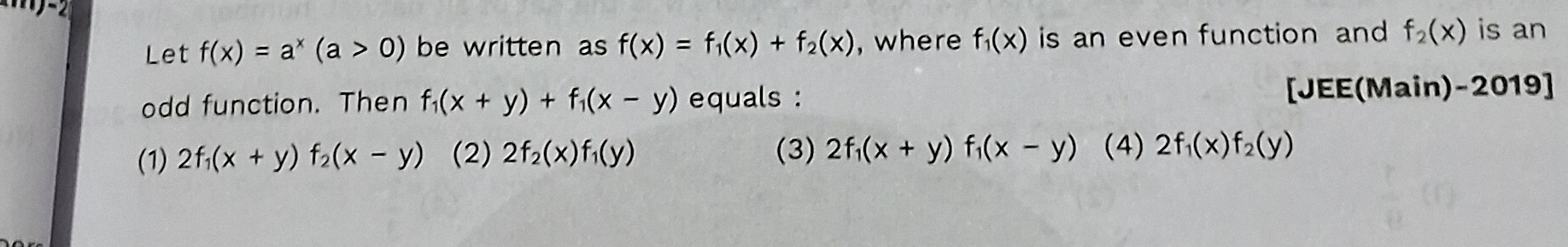
• A. 2f1(x + y) f2(x - y)
• B. 2f2(x)f1(y)
• C. 2f1(x + y) f1(x - y)
• D. 2f1(x)f2(y)

Answer 1

Answer: (B)

2f2(x)f1(y)

Answer 2

Let $f(x) = a^x$ for $a > 0$.

We are given that $f(x) = f_1(x) + f_2(x)$, where $f_1(x)$ is an even function and $f_2(x)$ is an odd function.

The even part of $f(x)$ is $f_1(x) = \frac{f(x) + f(-x)}{2}$.

The odd part of $f(x)$ is $f_2(x) = \frac{f(x) - f(-x)}{2}$.

For $f(x) = a^x$, we have $f(-x) = a^{-x}$.

So, $f_1(x) = \frac{a^x + a^{-x}}{2}$ and $f_2(x) = \frac{a^x - a^{-x}}{2}$.

The question asks for $f_1(x+y) + f_1(x-y)$. However, the options do not match the correct result for this expression. It is highly probable that there is a typo in the question, and it was intended to ask for $f_2(x+y) + f_2(x-y)$.

Assuming the question intended to ask for $f_2(x+y) + f_2(x-y)$:

$f_2(x+y) = \frac{a^{x+y} - a^{-(x+y)}}{2} = \frac{a^{x+y} - a^{-x-y}}{2}$.

$f_2(x-y) = \frac{a^{x-y} - a^{-(x-y)}}{2} = \frac{a^{x-y} - a^{-x+y}}{2}$.

$f_2(x+y) + f_2(x-y) = \frac{a^{x+y} - a^{-x-y} + a^{x-y} - a^{-x+y}}{2}$

$= \frac{(a^x a^y - a^{-x} a^y) + (a^x a^{-y} - a^{-x} a^{-y})}{2}$

$= \frac{a^y(a^x - a^{-x}) + a^{-y}(a^x - a^{-x})}{2}$

$= \frac{(a^y + a^{-y})(a^x - a^{-x})}{2}$

$= \left(\frac{a^y + a^{-y}}{2}\right) (a^x - a^{-x})$

$= f_1(y) (2f_2(x))$

$= 2f_2(x)f_1(y)$.

This matches option (2).