Question

Let $f(x) = 6x^{4/3} - 3x^{1/3}, x \in [-1, 1]$. Then

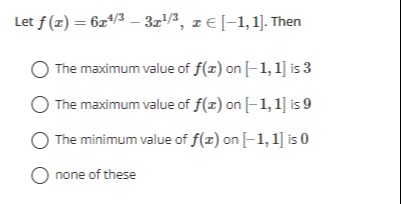
• A. The maximum value of $f(x)$ on $[-1, 1]$ is 3
• B. The maximum value of $f(x)$ on $[-1, 1]$ is 9
• C. The minimum value of $f(x)$ on $[-1, 1]$ is 0
• D. none of these

Answer 1

Answer: (B)

The maximum value of f(x) on [-1, 1] is 9

Answer 2

To find the maximum and minimum values of the function $f(x) = 6x^{4/3} - 3x^{1/3}$ on the interval $[-1, 1]$, we find the critical points by taking the derivative and setting it to zero.

$f'(x) = 8x^{1/3} - x^{-2/3} = \frac{8x - 1}{x^{2/3}}$

Critical points occur when $f'(x) = 0$ or is undefined. Thus, $x = \frac{1}{8}$ and $x = 0$ are critical points. We also evaluate the function at the endpoints $x = -1$ and $x = 1$.

$f(-1) = 6(-1)^{4/3} - 3(-1)^{1/3} = 6(1) - 3(-1) = 9$

$f(0) = 6(0)^{4/3} - 3(0)^{1/3} = 0$

$f\left(\frac{1}{8}\right) = 6\left(\frac{1}{8}\right)^{4/3} - 3\left(\frac{1}{8}\right)^{1/3} = 6\left(\frac{1}{16}\right) - 3\left(\frac{1}{2}\right) = \frac{3}{8} - \frac{12}{8} = -\frac{9}{8}$

$f(1) = 6(1)^{4/3} - 3(1)^{1/3} = 6 - 3 = 3$

Comparing the values $9, 0, -\frac{9}{8}, 3$, the maximum value is $9$ and the minimum value is $-\frac{9}{8}$.