Question

Let $f(x) = (1 + x)\ln(1 + x) - x - \frac{x^2}{4}$, $\forall x > -1$ and $f'(x) > 0$ $\forall x \in (0, \alpha)$, then maximum value of $[\alpha]$ is (where $[\,]$ denotes greatest integer function)

Answer 1

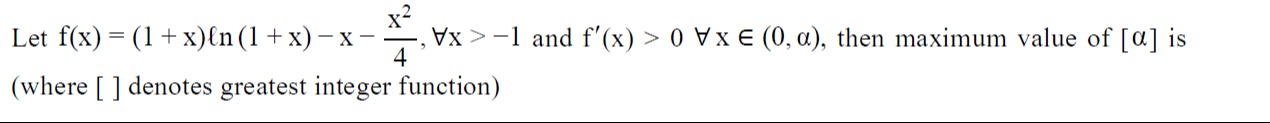
2

Answer 2

The problem asks us to find the maximum value of $[\alpha]$ such that $f'(x) > 0$ for all $x \in (0, \alpha)$, where $f(x) = (1 + x)\ln(1 + x) - x - \frac{x^2}{4}$.

First, we need to find the derivative of $f(x)$, denoted as $f'(x)$. The function is $f(x) = (1 + x)\ln(1 + x) - x - \frac{x^2}{4}$. Using the product rule for the first term and power rule for the others: $\frac{d}{dx}((1 + x)\ln(1 + x)) = \frac{d}{dx}(1 + x) \cdot \ln(1 + x) + (1 + x) \cdot \frac{d}{dx}(\ln(1 + x))$ $= 1 \cdot \ln(1 + x) + (1 + x) \cdot \frac{1}{1 + x}$ $= \ln(1 + x) + 1$

Now, differentiating the rest of the terms: $\frac{d}{dx}(-x) = -1$ $\frac{d}{dx}(-\frac{x^2}{4}) = -\frac{2x}{4} = -\frac{x}{2}$

Combining these, we get $f'(x)$: $f'(x) = (\ln(1 + x) + 1) - 1 - \frac{x}{2}$ $f'(x) = \ln(1 + x) - \frac{x}{2}$

We are given that $f'(x) > 0$ for all $x \in (0, \alpha)$. This means we need to find the values of $x$ for which $\ln(1 + x) - \frac{x}{2} > 0$. Let's define a new function $g(x) = \ln(1 + x) - \frac{x}{2}$. We need to find the interval $(0, \alpha)$ where $g(x) > 0$.

First, let's evaluate $g(x)$ at $x=0$: $g(0) = \ln(1 + 0) - \frac{0}{2} = \ln(1) - 0 = 0 - 0 = 0$.

Next, let's find the derivative of $g(x)$, $g'(x)$, to analyze its behavior: $g'(x) = \frac{d}{dx}(\ln(1 + x)) - \frac{d}{dx}(\frac{x}{2})$ $g'(x) = \frac{1}{1 + x} - \frac{1}{2}$

To find critical points, set $g'(x) = 0$: $\frac{1}{1 + x} - \frac{1}{2} = 0$ $\frac{1}{1 + x} = \frac{1}{2}$ $1 + x = 2$ $x = 1$

Now, let's analyze the sign of $g'(x)$:

• For $x \in (-1, 1)$ (considering the domain $x > -1$), if $x < 1$, then $1+x < 2$, so $\frac{1}{1+x} > \frac{1}{2}$. This means $g'(x) = \frac{1}{1+x} - \frac{1}{2} > 0$. Thus, $g(x)$ is increasing on the interval $(-1, 1)$.
• For $x \in (1, \infty)$, if $x > 1$, then $1+x > 2$, so $\frac{1}{1+x} < \frac{1}{2}$. This means $g'(x) = \frac{1}{1+x} - \frac{1}{2} < 0$. Thus, $g(x)$ is decreasing on the interval $(1, \infty)$.

Since $g(0) = 0$ and $g(x)$ is increasing for $x \in (0, 1)$, $g(x)$ will be positive for $x \in (0, 1]$. Let's check the value of $g(1)$: $g(1) = \ln(1 + 1) - \frac{1}{2} = \ln(2) - \frac{1}{2}$. Since $\ln(2) \approx 0.693$ and $1/2 = 0.5$, $g(1) \approx 0.693 - 0.5 = 0.193 > 0$.

Since $g(1) > 0$ and $g(x)$ is decreasing for $x > 1$, there must be a value $x_0 > 1$ where $g(x_0) = 0$. Let's test integer values for $x$ greater than 1:

• For $x=2$: $g(2) = \ln(1 + 2) - \frac{2}{2} = \ln(3) - 1$. Since $e \approx 2.718$, $e^1 < 3$, so $\ln(3) > 1$. Thus, $g(2) = \ln(3) - 1 > 0$. (Approximate value: $1.0986 - 1 = 0.0986$)
• For $x=3$: $g(3) = \ln(1 + 3) - \frac{3}{2} = \ln(4) - 1.5$. Since $e^{1.5} = e\sqrt{e} \approx 2.718 \times 1.648 \approx 4.47 > 4$, so $\ln(4) < 1.5$. Thus, $g(3) = \ln(4) - 1.5 < 0$. (Approximate value: $1.386 - 1.5 = -0.114$)

Since $g(2) > 0$ and $g(3) < 0$, the root $x_0$ of $g(x) = 0$ must lie between 2 and 3. So, $2 < x_0 < 3$.

From the analysis, $g(x) > 0$ for $x \in (0, x_0)$. The problem states that $f'(x) > 0$ for all $x \in (0, \alpha)$. This means $\alpha$ is the largest value such that $f'(x)$ remains positive throughout the interval $(0, \alpha)$. Therefore, $\alpha = x_0$.

Since $2 < x_0 < 3$, we have $2 < \alpha < 3$. We need to find the maximum value of $[\alpha]$, where $[\,]$ denotes the greatest integer function. For any value of $\alpha$ such that $2 < \alpha < 3$, the greatest integer less than or equal to $\alpha$ is $[\alpha] = 2$. Therefore, the maximum value of $[\alpha]$ is 2.

The final answer is $\boxed{2}$.

Explanation of the solution:

1. Calculate $f'(x)$: Differentiate $f(x) = (1 + x)\ln(1 + x) - x - \frac{x^2}{4}$ to get $f'(x) = \ln(1 + x) - \frac{x}{2}$.
2. Analyze $f'(x) > 0$: Set $g(x) = f'(x) = \ln(1 + x) - \frac{x}{2}$. We need to find the interval $(0, \alpha)$ where $g(x) > 0$.
3. Evaluate $g(0)$: $g(0) = \ln(1) - 0 = 0$.
4. Analyze $g'(x)$: Calculate $g'(x) = \frac{1}{1 + x} - \frac{1}{2}$.
   • Set $g'(x) = 0$ to find critical points: $\frac{1}{1 + x} = \frac{1}{2} \implies 1 + x = 2 \implies x = 1$.
   • For $x \in (0, 1)$, $g'(x) > 0$, so $g(x)$ is increasing.
   • For $x \in (1, \infty)$, $g'(x) < 0$, so $g(x)$ is decreasing.
5. Find the root $x_0$: Since $g(0) = 0$, and $g(x)$ increases for $x \in (0,1)$, then decreases for $x > 1$, there must be another root $x_0 > 1$.
   • $g(1) = \ln(2) - 0.5 \approx 0.193 > 0$.
   • $g(2) = \ln(3) - 1 \approx 0.0986 > 0$.
   • $g(3) = \ln(4) - 1.5 \approx -0.114 < 0$.
   • Since $g(2) > 0$ and $g(3) < 0$, the root $x_0$ lies between 2 and 3, i.e., $2 < x_0 < 3$.
6. Determine $\alpha$: $g(x) > 0$ for $x \in (0, x_0)$. The problem states $f'(x) > 0$ for all $x \in (0, \alpha)$, so $\alpha = x_0$.
7. Calculate $[\alpha]$: Since $2 < \alpha < 3$, the greatest integer less than or equal to $\alpha$ is $[\alpha] = 2$.

The maximum value of $[\alpha]$ is 2.