Question
Question: Let f'(x) > 0 ∀ x ∈ R$^+$ where f: R$^+$ → R and f(x) + $\frac{1}{x}$ = f$^{-1}$($\frac{1}{f(x)}$) a...
Let f'(x) > 0 ∀ x ∈ R+ where f: R+ → R and f(x) + x1 = f−1(f(x)1) and f−1(f(x)1) > 0. If sin−1(f(2)) is λ−π then 'λ' equals
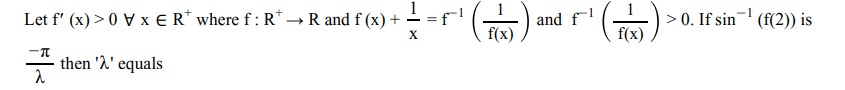
10
Solution
The given equation is f(x)+x1=f−1(f(x)1).
We are also given that f′(x)>0 for all x∈R+. This implies that f(x) is strictly increasing, so it is a one-to-one function and its inverse f−1(x) exists.
To simplify the functional equation, apply f to both sides:
f(f(x)+x1)=f(f−1(f(x)1))
f(f(x)+x1)=f(x)1
Let's assume a solution of the form f(x)=xc for some constant c.
First, let's check the condition f′(x)>0:
f′(x)=dxd(xc)=−x2c.
For f′(x)>0 for x∈R+, we must have −c>0, which means c<0.
Now, substitute f(x)=xc into the functional equation f(f(x)+x1)=f(x)1:
Left Hand Side (LHS):
f(f(x)+x1)=f(xc+x1)=f(xc+1)
Using f(x)=xc, we get:
f(xc+1)=xc+1c=c+1cx
Right Hand Side (RHS):
f(x)1=xc1=cx
Equating LHS and RHS:
c+1cx=cx
Since x∈R+, we can divide by x:
c+1c=c1
Cross-multiply:
c2=c+1
c2−c−1=0
This is a quadratic equation for c. Using the quadratic formula:
c=2(1)−(−1)±(−1)2−4(1)(−1)
c=21±1+4
c=21±5
We established earlier that c<0. Therefore, we must choose the negative root:
c=21−5
So the function is f(x)=2x1−5.
Now, let's check the condition f−1(f(x)1)>0.
For f(x)=xc, its inverse f−1(y) is found by letting y=xc⟹x=yc. So f−1(y)=yc.
Then f−1(f(x)1)=f−1(cx)=cxc=xc2.
We need xc2>0. Since x∈R+, we need c2>0.
Our value c=21−5 is not zero, so c2=(21−5)2=41+5−25=46−25=23−5.
Since 3>5 (as 9>5), 3−5>0. Thus c2>0, and the condition is satisfied.
Now we need to find sin−1(f(2)).
Substitute x=2 into f(x):
f(2)=2(2)1−5=41−5
We need to calculate sin−1(41−5).
Recall the known trigonometric value sin(10π)=sin(18∘)=45−1.
Therefore, sin−1(45−1)=10π.
Since 41−5=−(45−1), and sin−1(−y)=−sin−1(y):
sin−1(41−5)=−sin−1(45−1)=−10π.
We are given that sin−1(f(2))=λ−π.
So, −10π=λ−π.
Comparing both sides, we find λ=10.
