Question

Let $f:R \rightarrow R$ be a function such that $f(2)=4$ and $f'(2)=1$. Then, the value of $\lim_{x \to 2} \frac{x^2f(2)-4f(x)}{x-2}$ is equal to:

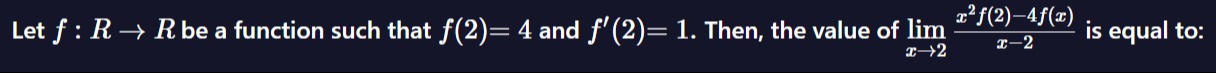
• A. 12
• B. 16
• C. 4
• D. 8

Answer 1

Answer: (A)

12

Answer 2

The limit is of the form $\frac{0}{0}$. Using L'Hopital's Rule: $\lim_{x \to 2} \frac{x^2f(2)-4f(x)}{x-2} = \lim_{x \to 2} \frac{2xf(2)-4f'(x)}{1}$ Substituting $x=2$, $f(2)=4$, $f'(2)=1$: $= 2(2)(4) - 4(1) = 16 - 4 = 12$