Question
Question: Let $f(n) = n^2 + 100$. Compute the remainder when $\underbrace{f(f(\cdots f(f(1))\cdots))}_{2025 \t...
Let f(n)=n2+100. Compute the remainder when 2025 f′sf(f(⋯f(f(1))⋯)) is divided by 104.
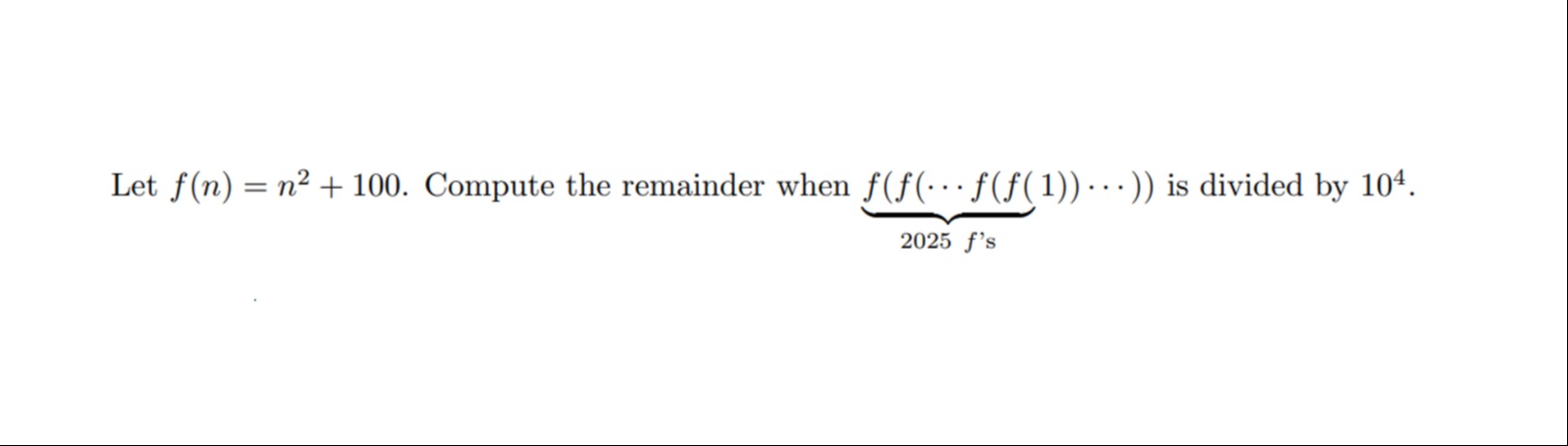
3101
Solution
Let the given function be f(n)=n2+100. We need to compute the remainder when 2025 f′sf(f(⋯f(f(1))⋯)) is divided by 104. Let x0=1. Let xk+1=f(xk)=xk2+100. We need to find x2025(mod104).
Let's compute the first few terms modulo 104: x0=1 x1=f(x0)=f(1)=12+100=101 x2=f(x1)=f(101)=1012+100=(100+1)2+100=(1002+2⋅100⋅1+12)+100 x2=10000+200+1+100=10301 x2≡301(mod10000)
x3=f(x2)=x22+100 x3≡3012+100(mod10000) 3012=(300+1)2=3002+2⋅300⋅1+12=90000+600+1=90601 x3≡90601+100(mod10000) x3≡90701(mod10000) x3≡701(mod10000)
x4=f(x3)=x32+100 x4≡7012+100(mod10000) 7012=(700+1)2=7002+2⋅700⋅1+12=490000+1400+1=491401 x4≡491401+100(mod10000) x4≡491501(mod10000) x4≡1501(mod10000)
Let's observe the pattern of xk(mod10000) for k≥1: x1≡101(mod10000) x2≡301(mod10000) x3≡701(mod10000) x4≡1501(mod10000)
It appears that xk≡100ak+1(mod10000) where ak follows a pattern. a1=1 a2=3 a3=7 a4=15 This suggests ak=2k−1.
Let's prove this by induction. Base case: For k=1, a1=21−1=1. This holds for x1=101. Inductive step: Assume xk≡100(2k−1)+1(mod10000) for some k≥1. Then xk+1=xk2+100. Substitute the assumed form of xk: xk+1≡(100(2k−1)+1)2+100(mod10000) Using (A+B)2=A2+2AB+B2: xk+1≡(100(2k−1))2+2⋅100(2k−1)⋅1+12+100(mod10000) xk+1≡10000(2k−1)2+200(2k−1)+1+100(mod10000) Since 10000(2k−1)2 is a multiple of 10000, it becomes 0(mod10000). xk+1≡200(2k−1)+101(mod10000) xk+1≡200⋅2k−200+101(mod10000) xk+1≡100⋅2⋅2k−99(mod10000) xk+1≡100⋅2k+1−99(mod10000) xk+1≡100(2k+1−1)+1(mod10000) This completes the induction. So, xk≡100(2k−1)+1(mod10000) for k≥1.
We need to compute x2025(mod10000). Using the formula for k=2025: x2025≡100(22025−1)+1(mod10000) x2025≡100⋅22025−100+1(mod10000) x2025≡100⋅22025−99(mod10000)
To evaluate this, we need to find 22025(mod100). We can use the Chinese Remainder Theorem since 100=4×25.
-
Modulo 4: Since 2025≥2, 22025 is divisible by 4. So, 22025≡0(mod4).
-
Modulo 25: We use Euler's totient theorem. ϕ(25)=25(1−1/5)=20. So, 220≡1(mod25). Now, we find the exponent 2025(mod20): 2025=20×101+5. So, 22025=(220)101⋅25≡1101⋅25(mod25) 25=32. 22025≡32(mod25) 22025≡7(mod25).
Now we have a system of congruences: Let N=22025. N≡0(mod4) N≡7(mod25)
From the second congruence, N=25k+7 for some integer k. Substitute this into the first congruence: 25k+7≡0(mod4) k+3≡0(mod4) (since 25≡1(mod4) and 7≡3(mod4)) k≡−3(mod4) k≡1(mod4) So k=4m+1 for some integer m. Substitute k back into the expression for N: N=25(4m+1)+7=100m+25+7=100m+32. Therefore, 22025≡32(mod100).
Finally, substitute this result back into the expression for x2025: x2025≡100⋅22025−99(mod10000) Let 22025=100m+32. x2025≡100(100m+32)−99(mod10000) x2025≡10000m+3200−99(mod10000) x2025≡3200−99(mod10000) x2025≡3101(mod10000)
The remainder is 3101.
