Question
Question: Let f(n) = $\frac{4n + \sqrt{4n^2-1}}{\sqrt{2n+1}+\sqrt{2n-1}}$ and $\lim_{n\to\infty} (\frac{f(1)+f...
Let f(n) = 2n+1+2n−14n+4n2−1 and limn→∞(1+2+3+....+nf(1)+f(2)+....f(n)) is equal to α then the value of 27α2 is:
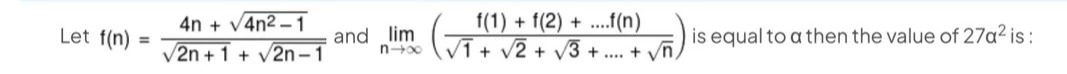
243/2
Solution
Solution Overview:
-
Simplify f(n):
f(n)=2n+1+2n−14n+4n2−1.
WriteMultiply numerator and denominator by 2n+1−2n−1 noting that (2n+1+2n−1)(2n+1−2n−1)=2. This gives
f(n)=21[(4n+4n2−1)(2n+1−2n−1)]. -
Express in Telescoping Form:
4n2−1=(2n−1)(2n+1).
Recognize thatWith some algebraic manipulation, the expression simplifies to
f(n)=21[(2n+1)2n+1−(2n−1)2n−1].This is a telescoping term.
-
Sum the Series:
SN=n=1∑Nf(n)=21[(2N+1)2N+1−(2⋅1−1)1]=21[(2N+1)2N+1−1].
Sum f(n) from n=1 to N: -
Estimate the Denominator:
DN≈∫0Nxdx=32N3/2.
The denominator DN=1+2+⋯+N for large N can be approximated by the integral: -
Compute the Limit:
SN∼21(2N⋅2N)=2N3/2.
For large N,Therefore,
α=N→∞limDNSN∼32N3/22N3/2=232. -
Final Calculation:
27α2=27(232)2=27⋅49⋅2=27⋅418=227⋅9=2243.
Finally, compute
Answer:
2243
Subject: Mathematics (NCERT Class XII, Chapter: Sequences and Series, Topic: Telescoping Series)
Difficulty Level: Medium
Question Type: fill_in_the_blank
