Question

Let $f,g:N \rightarrow N$ such that $f(n+1) = f(n)+f(1) \forall n \in N$ and g be any arbitrary function.

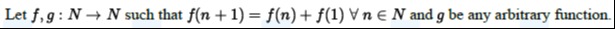
Answer 1

f(n) = n*f(1) for all n in N, and g is arbitrary.

Answer 2

Since

$$f(n+1) = f(n) + f(1) \quad \text{for all } n \in \mathbb{N},$$

the difference $f(n+1) - f(n) = f(1)$ is constant. This shows that $f(n)$ forms an arithmetic progression with common difference $f(1)$. Thus, by induction or by the formula for an arithmetic series, we have:

$$f(n) = n \cdot f(1) \quad \text{for all } n \in \mathbb{N}.$$

The function $g$ is given to be arbitrary so no restrictions are imposed on it.