Question

Let $f:(0,\infty)\to R$ be a differentiable function satisfying $f(x)+e^{f(x)}=\frac{2}{x}-\ln x -1$. Find the number of integers in the range of $x$ satisfying the inequality $f(2x^2+1)-f(x^2+5)\geq f(1), x>0$.

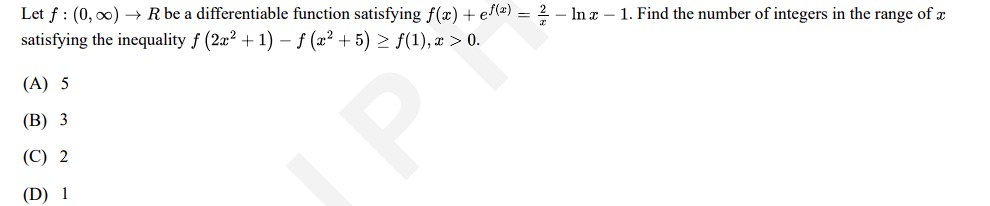
• A. 5
• B. 3
• C. 2
• D. 1

Answer 1

Answer: (C)

2

Answer 2

1. The function satisfies

   $f(x)+e^{f(x)}=\frac{2}{x}-\ln x-1$.

   Since the function $F(t)=t+e^t$ is strictly increasing, for any $y>0$ we have

   $f(y)=F^{-1}\Bigl[\frac{2}{y}-\ln y-1\Bigr]$.

2. To compare values $f(2x^2+1)$ and $f(x^2+5)$, note that if we can show that $f$ is strictly decreasing, then

   $f(2x^2+1) \ge f(x^2+5) \quad\text{if and only if}\quad 2x^2+1 \le x^2+5$.

3. Verify that $f$ is decreasing:

   Write $g(y)=\frac{2}{y}-\ln y$. Its derivative is

   $g'(y)=-\frac{2}{y^2}-\frac{1}{y}=-\frac{2+y}{y^2}<0,\quad y>0$.

   Therefore, $g(y)$ is decreasing, which implies that higher arguments yield lower values of $f$. Hence, $f$ is strictly decreasing.

4. Solve the inequality:

   $2x^2+1 \le x^2+5 \quad \Longrightarrow \quad x^2 \le 4$.

   Since $x>0$, we have:

   $0< x \le 2$.

5. The integer values of $x$ in this interval are $x=1$ and $x=2$. Therefore, there are 2 integers.

Core Explanation:

Since the function $f$ defined implicitly is shown to be decreasing, the inequality $f(2x^2+1)-f(x^2+5)\ge f(1)$ is equivalent to $2x^2+1\le x^2+5$, giving $x^2\le 4$ (i.e. $0<x\le 2$). The integers in $(0,2]$ are 1 and 2.