Solveeit Logo
Login

Question

Question: Let \(f(x) = {\mathop{\rm sgn}} ({\mathop{\rm sgn}} (x))\) . Then \(\mathop {\lim }\limits_{x \to 0}...

Let f(x)=sgn(sgn(x))f(x) = {\mathop{\rm sgn}} ({\mathop{\rm sgn}} (x)) . Then lim⁡x→0f(x)\mathop {\lim }\limits_{x \to 0} f(x) is:-
A) 1
B) 2
C) 0
D) Does not exist

Explanation

Solution

Here in this question the concept of signum function and limit will get used. Definition of signum function and limit existence is as follows:-
Signum function or sign function is defined as f(x) = ∣x∣x;x≠0\dfrac{{\left| x \right|}}{x};x \ne 0
f(x) = \left\\{ {\begin{array}{*{20}{c}} { - 1,x < 0}\\\ {0,x = 0}\\\ {1,x > 0} \end{array}} \right\\} is called a signum function.
Limit of a function exists when lim⁡x→0−f(x)=lim⁡x→0+f(x)=L\mathop {\lim }\limits_{x \to {0^ - }} f(x)\mathop { = \lim }\limits_{x \to {0^ + }} f(x) = L which is left hand side limit and right hand side limit and L=lim⁡x→0f(x)L = \mathop {\lim }\limits_{x \to 0} f(x)

Complete step-by-step answer:
As the given function is f(x)=sgn(sgn(x))f(x) = {\mathop{\rm sgn}} ({\mathop{\rm sgn}} (x)) so, first of all we will find the left hand side limit.
⇒lim⁡x→0−f(x)=sgn(sgn(0−))\Rightarrow \mathop {\lim }\limits_{x \to {0^ - }} f(x) = {\mathop{\rm sgn}} ({\mathop{\rm sgn}} ({0^ - }))
Now from the definition of signum function we know that sgn(x)=−1{\mathop{\rm sgn}} (x) = - 1 when x<0x < 0therefore we will get,
⇒lim⁡x→0−f(x)=sgn(−1)\Rightarrow \mathop {\lim }\limits_{x \to {0^ - }} f(x) = {\mathop{\rm sgn}} ( - 1)
For all values less than 0 signum functions will give -1
⇒lim⁡x→0−f(x)=−1\Rightarrow \mathop {\lim }\limits_{x \to {0^ - }} f(x) = - 1
Now we will find the right hand side limit.
⇒lim⁡x→0+f(x)=sgn(sgn(0+))\Rightarrow \mathop {\lim }\limits_{x \to {0^ + }} f(x) = {\mathop{\rm sgn}} ({\mathop{\rm sgn}} ({0^ + }))
Now from the definition of signum function we know that sgn(x)=1{\mathop{\rm sgn}} (x) = 1 when x>0x > 0therefore we will get,
⇒lim⁡x→0+f(x)=sgn(1)\Rightarrow \mathop {\lim }\limits_{x \to {0^ + }} f(x) = {\mathop{\rm sgn}} (1)
For all values greater than 0 signum function will give +1
⇒lim⁡x→0+f(x)=1\Rightarrow \mathop {\lim }\limits_{x \to {0^ + }} f(x) = 1
As we can see that left hand limit is not equal to the right hand limit therefore limit does not exist so the correct option is (D)

Note: Students may likely to make mistake while putting value of signum function so here below graphical approach for signum function is mentioned:-

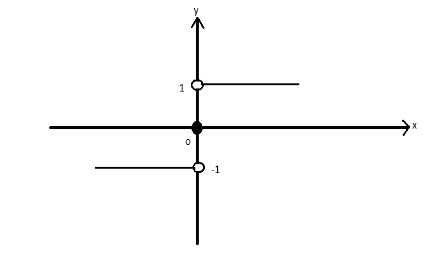
Here we can see that for x greater than zero the value of the function is 1 and for x less than zero the value of function is -1 and at x equal to zero value is zero. Also at points 1 and -1 there is a point of discontinuity as the graph breaks at these points.