Question

Let $f(x)=\ln mx(m>0)$ and $g(x)=px$ . Then the equation $\left| f(x) \right|=g(x)$ has exactly three solutions for
(a) $p=\dfrac{m}{e}$
(b) $0 < p < \dfrac{m}{e}$
(c) $0 < p< \dfrac{e}{m}$
(d) $p < \dfrac{e}{m}$

Answer 1

Hint: In the given question we have given equations of two curves out of which one is passing through origin and a given condition according to which the curve and the line has the same calculated value of the dependent variable. We will try to find the equation of the line tangent to the given curve and then plot the curve, line and the tangent, which will give us the area in which the feasible solution exists.

Complete step-by-step answer:
We have been given
$f(x)=\ln mx(m > 0)...............(i)$
Which is an equation of curve, and,
$g(x)=px...........(ii)$
This is an equation of straight line passing through the origin, as we know y = ax is a straight line passing through the origin.
Let us assume a point P(h, k) on the curve $f(x)=\ln mx$. Therefore, at point P, the equation for the curve f(x) can be written by substituting the values of P(h, k) in equation (i), we get
$\begin{aligned} & f(h)=\ln mh=k \\\ & \Rightarrow k=\ln mh..............(iii) \\\ \end{aligned}$
The slope of the curve f(x) at point P is given by,
$\begin{aligned} & f'(h,k)={{\left. \dfrac{d(\ln mx)}{dx} \right|}_{(h,k)}} \\\ & f'(h,k)={{\left. \dfrac{1}{mx}.m(1) \right|}_{(h,k)}} \\\ & f'(h,k)=\dfrac{1}{h}.................(iv) \\\ \end{aligned}$
Now, the equation line tangent to the curve f(x) at point can be written as,
$y-{{y}_{1}}=m(x-{{x}_{1}})..............(v)$
Here, ${{y}_{1}}=k,{{x}_{1}}=h$ and slope, $m=\dfrac{1}{h}$. Substituting the values in equation (v), we get
$\begin{aligned} & y-k=\dfrac{1}{h}(x-h) \\\ & \Rightarrow y-k=\dfrac{x}{h}-1.................(vi) \\\ \end{aligned}$
Now, it has been given $\left| f(x) \right|=g(x)$ , that means the curve f(x) also passes through the origin as g(x) passes through origin. So, the equation (vi) reduces to,
$\begin{aligned} & 0-k=\dfrac{1}{h}(0-h) \\\ & \Rightarrow -k=\dfrac{-h}{h} \\\ & \Rightarrow k=1.....................(a) \\\ \end{aligned}$
And substituting this value in equation (iii) gives
$1=\ln mh$
Taking antilog on both sides, we get
$\begin{aligned} & e=mh \\\ & \Rightarrow h=\dfrac{e}{m}.....................(b) \\\ \end{aligned}$
Putting the values from equation (a) and (b) in equation (vi), the general equation of line tangent to f(x) can be written as,
$\begin{aligned} & y-1=\dfrac{mx}{e}-1 \\\ & \Rightarrow y=\dfrac{mx}{e} \\\ \end{aligned}$
Now plotting the curve f(x), line g(x) and tangent ‘y’ on graph, we get

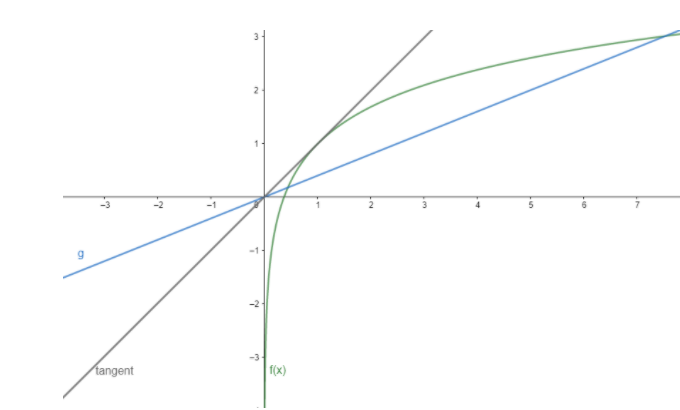
From the graph, we can see that for all the values,
$0 < p < \dfrac{m}{e}$
The condition satisfies the given line and curve and has an area enclosed by three curves.
Hence, the final answer is (b).

Note: The caution must be taken when interpreting the results from the graph and the curves satisfying the equations. Students often get confused after the step, $1=\ln mh$, they forget to antilog to solve this and get stuck.