Question
Question: Let f (x) is a non-zero differentiable function $\forall$ x $\in$ R & satisfying f (x + y) = f (x - ...
Let f (x) is a non-zero differentiable function ∀ x ∈ R & satisfying f (x + y) = f (x - y) ∀ x, y ∈ R, then -
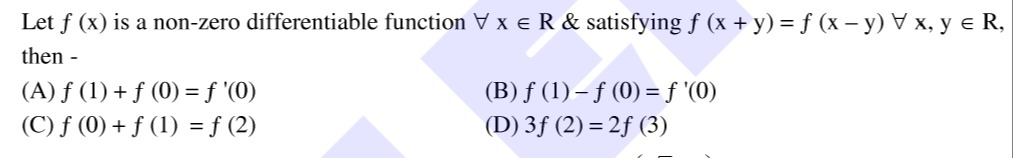
f (1) + f (0) = f '(0)
f (1) - f (0) = f '(0)
f (0) + f (1) = f (2)
3f (2) = 2f (3)
(B)
Solution
The given functional equation is f(x+y)=f(x−y) for all x,y∈R.
The function f(x) is a non-zero differentiable function for all x∈R.
Differentiate the given equation with respect to y: ∂y∂f(x+y)=∂y∂f(x−y)
Using the chain rule, this gives f′(x+y)⋅∂y∂(x+y)=f′(x−y)⋅∂y∂(x−y).
f′(x+y)⋅1=f′(x−y)⋅(−1)
f′(x+y)=−f′(x−y) (Equation 1)
Differentiate the given equation with respect to x: ∂x∂f(x+y)=∂x∂f(x−y)
Using the chain rule, this gives f′(x+y)⋅∂x∂(x+y)=f′(x−y)⋅∂x∂(x−y).
f′(x+y)⋅1=f′(x−y)⋅1
f′(x+y)=f′(x−y) (Equation 2)
From Equation 1 and Equation 2, we have:
−f′(x−y)=f′(x−y)
2f′(x−y)=0
f′(x−y)=0 for all x,y∈R.
Let z=x−y. Since x and y can be any real numbers, z can also be any real number.
Thus, f′(z)=0 for all z∈R.
Since the derivative of f(x) is zero for all x, f(x) must be a constant function.
Let f(x)=c for some constant c.
The problem states that f(x) is a non-zero function, so c=0.
Now we check which of the given options is true for f(x)=c where c=0, and f′(x)=0.
(A) f(1)+f(0)=f′(0)
Substituting the values, we get c+c=0, which simplifies to 2c=0. This implies c=0, which contradicts the condition c=0. So, option (A) is incorrect.
(B) f(1)−f(0)=f′(0)
Substituting the values, we get c−c=0, which simplifies to 0=0. This statement is true for any value of c, including any non-zero constant c. So, option (B) is correct.
(C) f(0)+f(1)=f(2)
Substituting the values, we get c+c=c, which simplifies to 2c=c, or c=0. This contradicts the condition c=0. So, option (C) is incorrect.
(D) 3f(2)=2f(3)
Substituting the values, we get 3c=2c, which simplifies to c=0. This contradicts the condition c=0. So, option (D) is incorrect.
The only option that is true for any non-zero differentiable function satisfying the given functional equation is (B).
