Question

Let f: R→R be defined by $f(x) = \frac{x}{1+x^2}$, $x \in R$. Then the range of f is:

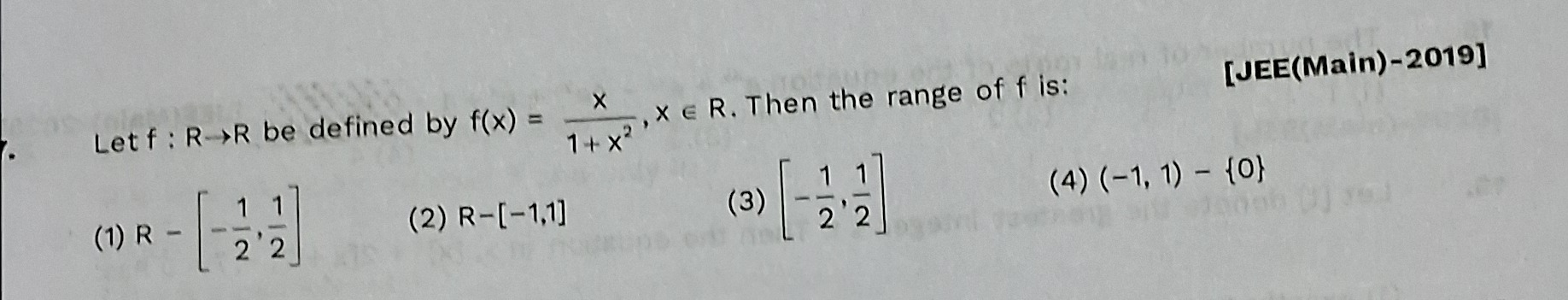
• A. R - $[-\frac{1}{2}, \frac{1}{2}]$
• B. R-[-1,1]
• C. $[-\frac{1}{2}, \frac{1}{2}]$
• D. (-1, 1) - {0}

Answer 1

Answer: (C)

$[-\frac{1}{2}, \frac{1}{2}]$

Answer 2

Let $y = f(x) = \frac{x}{1+x^2}$. Rearrange to get $yx^2 - x + y = 0$.

If $y=0$, $x=0$ is a real solution.

If $y \neq 0$, this is a quadratic in $x$. For real solutions, the discriminant $\Delta = (-1)^2 - 4(y)(y) = 1 - 4y^2$ must be non-negative.

$1 - 4y^2 \ge 0 \implies 4y^2 \le 1 \implies y^2 \le \frac{1}{4} \implies -\frac{1}{2} \le y \le \frac{1}{2}$.

Combining the cases, the range is $[-\frac{1}{2}, \frac{1}{2}]$.