Question

Let f: R$\to$R and g: R$\to$R be respectively given by f(x) = |x| + 1 and g(x) =${x^2} + 1$. Define h: R$\to$R by
h(x) = \left\\{ \begin{gathered} \max {\text{ }}\left\\{ {f\left( x \right),g\left( x \right)} \right\\}{\text{ if }}x \leqslant 0 \\\ \min {\text{ }}\left\\{ {f\left( x \right),g\left( x \right)} \right\\}{\text{ if }}x > 0 \\\ \end{gathered} \right..
Then number of points at which h(x) is not differentiable is

Answer 1

In this question find the meeting points of function f(x) and function g(x) and also remember to use the graphical representation of the given functions, use this information to approach towards the solution of the question.

Complete step by step answer:
According to the given information we have function f(x) = |x| + 1 and g(x) = ${x^2} + 1$ where f: R$\to$R and g: R$\to$R
So for function f(x) = |x|+1 = \left\\{ \begin{gathered} f\left( x \right) = x + 1{\text{ for }}x \geqslant 0 \\\ f\left( x \right) = - x + 1{\text{ for }}x < 0 \\\ \end{gathered} \right.
For the function g(x) = ${x^2} + 1$ we know that for $x \geqslant 0$ and for x < 0 the function g(x) = ${x^2} + 1$
Finding the meeting point for function f(x) and function g(x)
When x < 0
Function f(x) = - x + 1 and function g(x) = ${x^2} + 1$
We know that at the meeting point of two function f(x) = g(x)
Therefore ${x^2} + 1$ = - x + 1
$\Rightarrow$ ${x^2} + x = 1 - 1$
$\Rightarrow$x (x+1) = 0
Since x can’t be 0 therefore x = - 1
For x = -1, y = 2
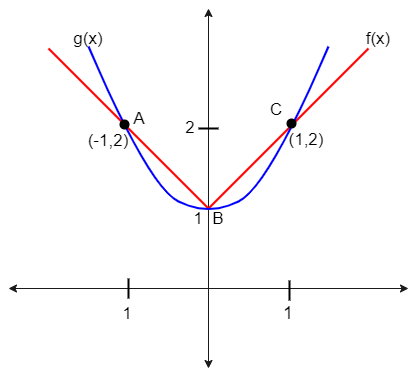
Therefore the function f(x) and function g(x) for x < 0 will meet at (-1, 2)
For $x \geqslant 0$
Function f(x) = x + 1 and function g(x) = ${x^2} + 1$
We know that at the meeting point f(x) = g(x)
Therefore x + 1 = ${x^2} + 1$
$\Rightarrow$ ${x^2} - x = 1 - 1$
$\Rightarrow$x(x – 1) = 0
Therefore x = 0, 1
For x = 0, y = 1
And for x =1, y = 2
Therefore function f(x) and function g(x) for $x \geqslant 0$ will meet at (0, 1) and (1, 2)
The graphical representation of the above equation is given below

For function h(x) we know that h(x) = \left\\{ \begin{gathered} \max {\text{ }}\left\\{ {f\left( x \right),g\left( x \right)} \right\\}{\text{ if }}x \leqslant 0 \\\ \min {\text{ }}\left\\{ {f\left( x \right),g\left( x \right)} \right\\}{\text{ if }}x > 0 \\\ \end{gathered} \right.

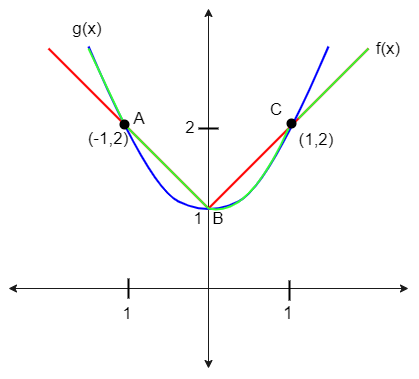
Here green shows the representation of h(x) function
We know that for $x \leqslant 0$the function h(x) is maximum so in the above graph
For x < -1 function g(x) is showing the maximum value
For – 1 < x < 0 function f(x) is showing the maximum value
Also for x > 0 the function h(x) is minimum do by the above graph
For 0 < x < 1 function g(x) is showing the minimum value
And for x > 1 function f(x) is showing the minimum value
So by the above statement we can say that function h(x) is not differentiable at (0, 1), (-1, 2) and (1, 2)
Hence the number of points at which h(x) is not differentiable at 3 points.

Note: In the above solution we used a term “function” which can be explained as a relation between the set of inputs and the set of possible outputs of those inputs. A function is represented as f: X $\to$Y Here X and Y are the two types of variables i.e. independent and dependent variables, thus this function defines the relationship between X and Y.