Question

Let $f: R \rightarrow (-\infty, 4]$ be a function defined as $f(x) = -x^2 + 8px + 8 + 2p - 16p^2$ be a surjective function on $R$, then the value of $p$ is equal to:

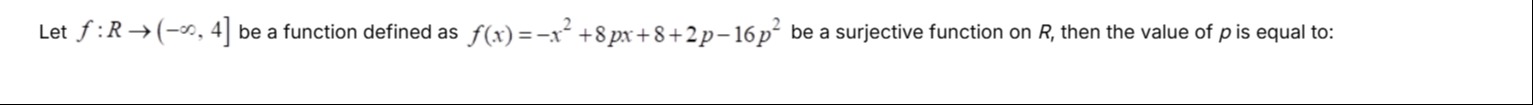
Answer 1

-2

Answer 2

The function is a downward-opening parabola, so its range is $(-\infty, \text{maximum value}]$. For the function to be surjective onto $(-\infty, 4]$, its maximum value must be 4. The maximum value of $f(x) = -x^2 + 8px + 8 + 2p - 16p^2$ occurs at $x = -b/(2a) = -8p/(2(-1)) = 4p$. Substituting $x=4p$ into $f(x)$ gives the maximum value: $f(4p) = -(4p)^2 + 8p(4p) + 8 + 2p - 16p^2 = -16p^2 + 32p^2 + 8 + 2p - 16p^2 = 2p + 8$. Equating this to 4: $2p + 8 = 4 \implies 2p = -4 \implies p = -2$.