Question

Let $f: R-\{2\} \rightarrow R-\{2\}$ be a function such that $f(x) = \frac{2x-1}{x-2}$, $(x \ne 2)$ then $f(x)$ is

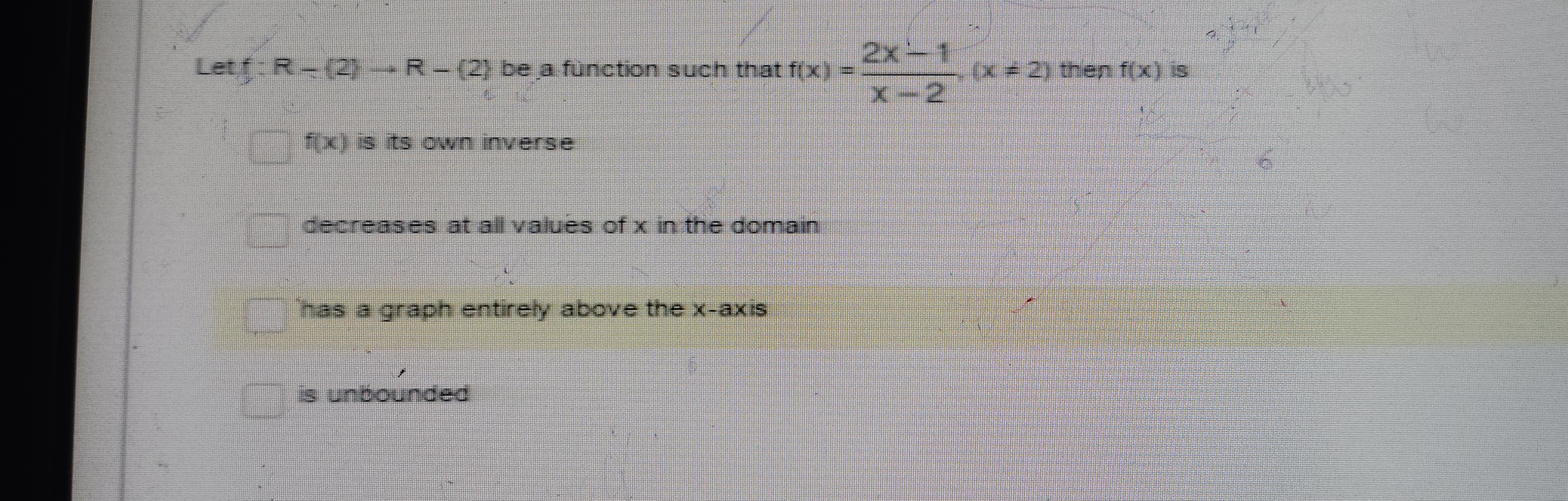
• A. f(x) is its own inverse
• B. decreases at all values of x in the domain
• C. has a graph entirely above the x-axis
• D. is unbounded

Answer 1

Answer: (A), (B), (D)

f(x) is its own inverse, decreases at all values of x in the domain, is unbounded

Answer 2

Let the function be $f(x) = \frac{2x-1}{x-2}$ with domain $R-\{2\}$ and codomain $R-\{2\}$.

Let's analyze each option:

1. $f(x)$ is its own inverse:

To check if $f(x)$ is its own inverse, we need to verify if $f(f(x)) = x$.

$f(f(x)) = f\left(\frac{2x-1}{x-2}\right)$

Substitute $x$ with $\frac{2x-1}{x-2}$ in the expression for $f(x)$:

$f\left(\frac{2x-1}{x-2}\right) = \frac{2\left(\frac{2x-1}{x-2}\right)-1}{\left(\frac{2x-1}{x-2}\right)-2}$

To simplify, multiply the numerator and denominator by $(x-2)$:

$= \frac{2(2x-1) - 1(x-2)}{(2x-1) - 2(x-2)}$

$= \frac{4x-2 - x+2}{2x-1 - 2x+4}$

$= \frac{3x}{3}$

$= x$

Since $f(f(x)) = x$ for all $x$ in the domain, the function $f(x)$ is its own inverse. This option is correct.

2. $f(x)$ decreases at all values of x in the domain:

To determine if the function is decreasing, we examine its derivative $f'(x)$.

Using the quotient rule, $f'(x) = \frac{(x-2)\frac{d}{dx}(2x-1) - (2x-1)\frac{d}{dx}(x-2)}{(x-2)^2}$

$f'(x) = \frac{(x-2)(2) - (2x-1)(1)}{(x-2)^2}$

$f'(x) = \frac{2x-4 - 2x+1}{(x-2)^2}$

$f'(x) = \frac{-3}{(x-2)^2}$

The domain of the function is $R-\{2\}$. For any $x \in R-\{2\}$, $(x-2)^2 > 0$.

Therefore, $f'(x) = \frac{-3}{(x-2)^2} < 0$ for all $x \in R-\{2\}$.

The derivative is negative throughout the domain. This means the function is strictly decreasing on each connected component of its domain, i.e., on the interval $(-\infty, 2)$ and on the interval $(2, \infty)$.

The phrasing "decreases at all values of x in the domain" is sometimes interpreted as $f'(x) < 0$ for all $x$ in the domain. Under this interpretation, the option is correct.

However, strictly speaking, a function $f$ is decreasing on a set $S$ if for any $x_1, x_2 \in S$ with $x_1 < x_2$, we have $f(x_1) \ge f(x_2)$. Let's check this for the entire domain $R-\{2\}$. Consider $x_1 = 1$ and $x_2 = 3$. Both are in the domain, and $1 < 3$.

$f(1) = \frac{2(1)-1}{1-2} = \frac{1}{-1} = -1$.

$f(3) = \frac{2(3)-1}{3-2} = \frac{5}{1} = 5$.

Since $f(1) = -1 < f(3) = 5$, the function is not decreasing on the entire domain $R-\{2\}$.

Given the context of multiple correct options and the common usage in some exams, the interpretation $f'(x) < 0$ for all $x$ in the domain implying "decreases at all values of x in the domain" is likely intended. Under this interpretation, this option is correct.

3. Has a graph entirely above the x-axis:

For the graph to be entirely above the x-axis, $f(x) > 0$ for all $x$ in the domain.

$f(x) = \frac{2x-1}{x-2} > 0$.

This inequality holds when both numerator and denominator have the same sign.

Case 1: $2x-1 > 0$ and $x-2 > 0$. This means $x > 1/2$ and $x > 2$. Both conditions are satisfied when $x > 2$.

Case 2: $2x-1 < 0$ and $x-2 < 0$. This means $x < 1/2$ and $x < 2$. Both conditions are satisfied when $x < 1/2$.

So, $f(x) > 0$ when $x \in (-\infty, 1/2) \cup (2, \infty)$.

For values of $x$ between $1/2$ and $2$ (e.g., $x=1$), $f(x) = \frac{2(1)-1}{1-2} = \frac{1}{-1} = -1 < 0$.

Since there are values of $x$ in the domain for which $f(x)$ is negative, the graph is not entirely above the x-axis. This option is incorrect.

4. Is unbounded:

A function is unbounded if its range is an unbounded set. The range of the function $f: R-\{2\} \rightarrow R-\{2\}$ is given as $R-\{2\}$. The set $R-\{2\}$ consists of all real numbers except 2, which is $(-\infty, 2) \cup (2, \infty)$. This set is unbounded as it extends infinitely in both positive and negative directions (excluding the point 2).

Alternatively, we can check the behavior of the function near the vertical asymptote $x=2$.

$\lim_{x \to 2^+} f(x) = \lim_{x \to 2^+} \frac{2x-1}{x-2} = \frac{2(2)-1}{2^+ - 2} = \frac{3}{0^+} = +\infty$.

$\lim_{x \to 2^-} f(x) = \lim_{x \to 2^-} \frac{2x-1}{x-2} = \frac{2(2)-1}{2^- - 2} = \frac{3}{0^-} = -\infty$.

Since the function approaches $+\infty$ and $-\infty$, it is unbounded. This option is correct.

Based on the analysis, options 1, 2 (under the interpretation $f'(x) < 0$), and 4 are correct. Assuming the question intends the interpretation where $f'(x) < 0$ everywhere in the domain implies the decreasing property, all three options 1, 2, and 4 are correct.