Question

Let f: R→ [0, 1] be a function defined by f (x) = min (e-|x|, |x|2 - 1|). Identify which of the following option is correct?

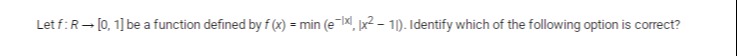
• A. f is differentiable at x = 0.
• B. f is differentiable at x = 1.
• C. f is differentiable at x = -1.
• D. f is differentiable at x = $\sqrt{2} - 1$

Answer 1

Answer: (D)

f is differentiable at x = $\sqrt{2} - 1$

Answer 2

The function is $f(x) = \min(e^{-|x|}, ||x|^2 - 1|)$.

1. Analyze differentiability:

• $f(x)$ is an even function, so we analyze for $x \ge 0$ and extend to $x < 0$.
• Let $g(x) = e^{-|x|}$ and $h(x) = ||x|^2 - 1|$.

2. Non-differentiability of g(x) or h(x):

• $g(x) = e^{-|x|}$ is not differentiable at $x = 0$ (cusp).
• $h(x) = |x^2 - 1|$ is not differentiable at $x^2 - 1 = 0$, i.e., $x = \pm 1$ (cusps).

3. Points where f(x) is not differentiable due to g(x) or h(x) being non-differentiable:

• At $x = 0$: $f(0) = \min(e^0, |0 - 1|) = \min(1, 1) = 1$.
  $f'(0^-) = \lim_{h \to 0^-} \frac{f(h) - f(0)}{h} = \lim_{h \to 0^-} \frac{e^{-|h|} - 1}{h} = \lim_{h \to 0^-} \frac{e^h - 1}{h} = 1$.
  $f'(0^+) = \lim_{h \to 0^+} \frac{f(h) - f(0)}{h} = \lim_{h \to 0^+} \frac{e^{-|h|} - 1}{h} = \lim_{h \to 0^+} \frac{e^{-h} - 1}{h} = -1$.
  Since $f'(0^-) \ne f'(0^+)$, $f(x)$ is not differentiable at $x = 0$.

• At $x = 1$: $f(1) = \min(e^{-1}, |1 - 1|) = \min(e^{-1}, 0) = 0$.
  For $x \in (0, 1)$, $h(x) = 1 - x^2$. For $x > 1$, $h(x) = x^2 - 1$.
  $f'(1^-) = \lim_{h \to 0^-} \frac{f(1 + h) - f(1)}{h}$. For $x$ slightly less than 1, $f(x) = 1 - x^2$. So $f'(1^-) = \frac{d}{dx}(1 - x^2)|_{x = 1} = -2$.
  $f'(1^+) = \lim_{h \to 0^+} \frac{f(1 + h) - f(1)}{h}$. For $x$ slightly greater than 1, $f(x) = x^2 - 1$. So $f'(1^+) = \frac{d}{dx}(x^2 - 1)|_{x = 1} = 2$.
  Since $f'(1^-) \ne f'(1^+)$, $f(x)$ is not differentiable at $x = 1$.

• At $x = -1$: By symmetry, $f(x)$ is not differentiable at $x = -1$.

4. Points where g(x) = h(x) and their derivatives are not equal:

We need to find the intersection points of $e^{-|x|}$ and $||x|^2 - 1|$.

• Case A: $0 \le x < 1$: $e^{-x} = 1 - x^2$.
  Let $k(x) = e^{-x} - (1 - x^2)$. $k(0) = 0$.
  $k'(x) = -e^{-x} + 2x$. Setting $k'(x) = 0$ gives $e^{-x} = 2x$.
  The solution to $e^{-x} = 2x$ is $x_c = \sqrt{2} - 1 \approx 0.414$.
  At $x_c = \sqrt{2} - 1$, $k(x_c) = e^{-x_c} - (1 - x_c^2) = 2x_c - (1 - x_c^2) = x_c^2 + 2x_c - 1$.
  Since $x_c = \sqrt{2} - 1$ is a root of $t^2 + 2t - 1 = 0$, $k(x_c) = 0$.
  This means $e^{-x_c} = 1 - x_c^2$ and their derivatives are equal: $g'(x_c) = -e^{-x_c}$ and $h'(x_c) = -2x_c$. Since $e^{-x_c} = 2x_c$, we have $-e^{-x_c} = -2x_c$.
  Thus, $f(x)$ is differentiable at $x = \sqrt{2} - 1$.

• Case B: $x \ge 1$: $e^{-x} = x^2 - 1$.
  Let $m(x) = e^{-x} - (x^2 - 1)$. $m(1) = e^{-1} - 0 = e^{-1} > 0$.
  As $x \to \infty$, $m(x) \to -\infty$.
  $m'(x) = -e^{-x} - 2x < 0$ for $x \ge 1$. So there is a unique root $x_I > 1$.
  At $x_I$, $g(x_I) = h(x_I)$.
  $g'(x_I) = -e^{-x_I}$. $h'(x_I) = 2x_I$.
  For differentiability, we need $-e^{-x_I} = 2x_I$.
  Substituting $e^{-x_I} = x_I^2 - 1$, we get $-(x_I^2 - 1) = 2x_I$, which simplifies to $x_I^2 + 2x_I - 1 = 0$.
  The positive solution is $x_I = \sqrt{2} - 1 \approx 0.414$.
  However, our $x_I$ is greater than 1. Since $\sqrt{2} - 1 \ne x_I$, their derivatives are not equal.
  Thus, $f(x)$ is not differentiable at $x = x_I$.

Conclusion:

The points where $f(x)$ is not differentiable are $x = 0$, $x = 1$, and $x = x_I$ (and their symmetric counterparts). However, $f(x)$ is differentiable at $x = \sqrt{2} - 1$.