Question

Let $f:\mathbb{R}\to \mathbb{R}$ be any function defining $g:\mathbb{R}\to \mathbb{R}$ by $g\left( x \right)=\left| f\left( x \right) \right|$ for all $x\in \mathbb{R}$ then g is
A. onto if f is into
B. one-one if f is one-one
C. continuous if f is continuous
D. differentiable if f is differentiable

Answer 1

The domain of the given function $g\left( x \right)=\left| f\left( x \right) \right|$ is real as $f:\mathbb{R}\to \mathbb{R}$. We try to form the modulus function and find the continuity of the curve. We assume the function $y=f\left( x \right)$ and put the values in the main function g. We show that $g\left( x \right)=\left| f\left( x \right) \right|$ is continuous as long as $f:\mathbb{R}\to \mathbb{R}$ and the domain of g is in real values.

Complete step-by-step answer:
In the function $g\left( x \right)=\left| f\left( x \right) \right|$, the main function is the modulus function.
Let’s check the continuity of $\left| y \right|$ for $y:\mathbb{R}\to \mathbb{R}$ where $y=f\left( x \right)$.
$\forall y\in \mathbb{R}$, we can put the graph of the modulus function as

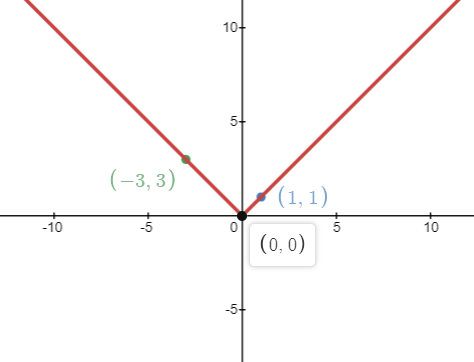
The graph of modulus is continuous itself. So, the condition for $\left| y \right|$ to be continuous $y\in \mathbb{R}$.
If there exists some y where $y\notin \mathbb{R}$, then $\left| y \right|$ is discontinuous.
Now it’s given that $f:\mathbb{R}\to \mathbb{R}$. So, the range of f is only real. So, all values of $y=f\left( x \right)$ are accounted for in the real value range.
So, $g\left( x \right)=\left| f\left( x \right) \right|$ is also continuous as $g:\mathbb{R}\to \mathbb{R}$.
The correct option is C.

So, the correct answer is “Option C”.

Note: The relation between continuity and differentiability is that if a function is differentiable then the function is definitely continuous. But the opposite is not always true. So, if we show that $y=f\left( x \right)$ is continuous, its differentiability is only known when we have the exact function. Now if we assume that $y=f\left( x \right)={{x}^{2}}$, then we can see that the function f is not one-one but the function g is one-one. So, all the other options were not considered. In case of the modulus function whatever be the function of the outer always remains continuous.