Solveeit Logo
Login

Question

Question: Let\(f\left( x \right) = x\sin \pi x,{\text{ }}x > 0\) . Then for all natural numbers \(n,{\text{ }}...

Letf(x)=xsin⁡πx, x>0f\left( x \right) = x\sin \pi x,{\text{ }}x > 0 . Then for all natural numbers n, f′(x)n,{\text{ }}f'\left( x \right) vanishes at:
(A). A unique point in the interval (n,n+12)\left( {n,n + \dfrac{1}{2}} \right)
(B). A unique point in the interval (n+12,n+1)\left( {n + \dfrac{1}{2},n + 1} \right)
(C). A unique point in the interval(n,n+1)\left( {n,n + 1} \right)
(D). Two points in the interval (n,n+1)\left( {n,n + 1} \right)

Explanation

Solution

Hint- To solve this question first we have to find the differentiation of the given function, then equate this to zero. and we get the required answer.

Complete step-by-step solution -

Now given that,
f(x)=xsin⁡πx, x>0f\left( x \right) = x\sin \pi x,{\text{ }}x > 0
And we have to find f′(x)f'\left( x \right)
Now to differentiate it we will apply product rule.
According to product rule,
d(uv)dx=udvdx+vdudx\dfrac{{d\left( {uv} \right)}}{{dx}} = u\dfrac{{dv}}{{dx}} + v\dfrac{{du}}{{dx}}
Now,
df(x)dx=f′(x)=sin⁡(πx)⋅dxdx+xdsin⁡(πx)dx or f′(x)=sin⁡(πx)+xdsin⁡(πx)d(πx)×d(πx)dx (By chain rule)  or f′(x)=sin⁡(πx)+xcos⁡(πx)⋅π or f′(x)=sin⁡(πx)+cos⁡πx(πx)  \dfrac{{df\left( x \right)}}{{dx}} = f'\left( x \right) = \sin \left( {\pi x} \right) \cdot \dfrac{{dx}}{{dx}} + x\dfrac{{d\sin \left( {\pi x} \right)}}{{dx}} \\\ {\text{or }}f'\left( x \right) = \sin \left( {\pi x} \right) + x\dfrac{{d\sin \left( {\pi x} \right)}}{{d\left( {\pi x} \right)}} \times \dfrac{{d\left( {\pi x} \right)}}{{dx}}{\text{ }}\left( {{\text{By chain rule}}} \right){\text{ }} \\\ {\text{or }}f'\left( x \right) = \sin \left( {\pi x} \right) + x\cos \left( {\pi x} \right) \cdot \pi \\\ {\text{or }}f'\left( x \right) = \sin \left( {\pi x} \right) + \cos \pi x\left( {\pi x} \right) \\\
Now we have to find f′(x)f'\left( x \right) vanishes at, for that we will put the value of f′(x)=0f'\left( x \right) = 0
f′(x)=sin⁡(πx)+cos⁡πx(πx)=0 or - [cos⁡(πx)]πx=sin⁡(πx) or sin⁡(πx)cos⁡(πx)=−πx or tan⁡(πx)=−πx  f'\left( x \right) = \sin \left( {\pi x} \right) + \cos \pi x\left( {\pi x} \right) = 0 \\\ {\text{or - }}\left[ {\cos \left( {\pi x} \right)} \right]\pi x = \sin \left( {\pi x} \right) \\\ {\text{or }}\dfrac{{\sin \left( {\pi x} \right)}}{{\cos \left( {\pi x} \right)}} = - \pi x \\\ {\text{or }}\tan \left( {\pi x} \right) = - \pi x \\\
Now let’s draw the graph of tan⁡(πx)=−πx\tan \left( {\pi x} \right) = - \pi x

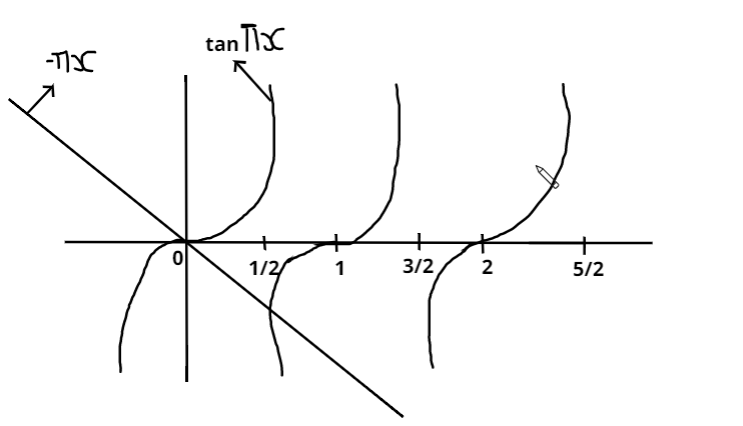
Now from the graph it is pretty much clear that −πx - \pi xline is cutting tan⁡πx\tan \pi x for every n+12n + \dfrac{1}{2} but nn belongs to natural number, so it would be cutting a unique point between (n+12,n+1)\left( {n + \dfrac{1}{2},n + 1} \right) because as we see that it first cuts between 12\dfrac{1}{2} to 11 then it again cuts somewhere at 32\dfrac{3}{2} and so on. Therefore there is a gap of 11
⇒πx∈(2n+12π,(n+1)π) ⇒x∈(n+12,n+1) and also x∈(n,n+1).  \Rightarrow \pi x \in \left( {\dfrac{{2n + 1}}{2}\pi ,\left( {n + 1} \right)\pi } \right) \\\ \Rightarrow x \in \left( {n + \dfrac{1}{2},n + 1} \right){\text{ and also }}x \in \left( {n,n + 1} \right). \\\
Therefore, the correct option will be (B) and (C).
Note- These types of questions can be solved by using the concept of maxima and minima. In this question we simply find the value of f′(x)f'\left( x \right) and then we observe it in the graph and we get our answer.