Question

Let $f\left( x \right){\text{ }} = {\text{ }}\left| {{\text{ }}cos{\text{ }}x{\text{ }}} \right|$ . Then,
A. $f$ is everywhere differentiable
B. $f$ is everywhere continuous but not differentiable at $n = n\pi ,n \in Z$
C. $f$ is everywhere continuous but not differentiable at $x = (2n + 1)\dfrac{\pi }{2},n \in Z$
D. None of these

Answer 1

The function $\left| {{\text{ }}cos{\text{ }}x{\text{ }}} \right|$ is given in mod which implies that it can be also written as $\cos x, - \cos x$ . The best method to solve this question is using the graph method in which we plot $\left| {{\text{ }}cos{\text{ }}x{\text{ }}} \right|$ as function and solve it . If while plotting a graph the tip of the pen is not held up then you can say it is continuous

Complete step by step answer:
Given : $\left| {{\text{ }}cos{\text{ }}x{\text{ }}} \right| = \cos x, - \cos x$ , on plotting graph of $\left| {{\text{ }}cos{\text{ }}x{\text{ }}} \right|$ , we get

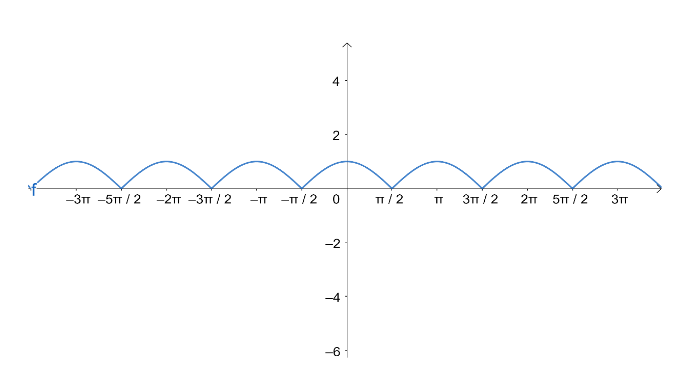
From the graph drawn we find that the function $\left| {{\text{ }}cos{\text{ }}x{\text{ }}} \right|$ is continuous everywhere as :
$f\left( x \right) = \left| {cos{\text{ }}x} \right|\;$
$\Rightarrow h\left( x \right) = \left| x \right|$
Let $g\left( x \right)$ be the function for $cos{\text{ }}x$ , therefore
$g\left( x \right) = cos{\text{ }}x$ , now solving the function for $h \circ g\left( x \right)$ , we get
$h \circ g\left( x \right) = \left| {\cos x} \right|$
Since , $cos{\text{ }}x$ is a continuous function f(c) must be defined . For the differentiability of $cos{\text{ }}x$ , the limit of the function as $x$ approaches the right hand limit ( RHL ) and left hand limit ( LHL ) there must exist a value $c$ . The function's value at c and the limit as $x$ approaches $c$ must be the same.The function $cos{\text{ }}x$ is every continuous and differentiable in its domain.

Therefore $\left| {{\text{ }}cos{\text{ }}x{\text{ }}} \right|$ is also continuous . Now , for differentiability we draw a tangent to the curve ,

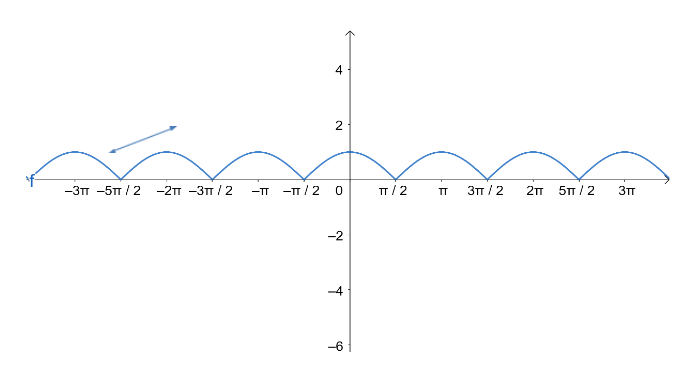
At $\left| {{\text{ }}cos{\text{ }}x{\text{ }}} \right|$ $= - 2\pi$ , therefore we can say that $\left| {{\text{ }}cos{\text{ }}x{\text{ }}} \right|$ is differentiable at $= - 2\pi$ . But at $\left| {{\text{ }}cos{\text{ }}x{\text{ }}} \right|$ $= \dfrac{\pi }{2}$ , we were not able to draw a tangent at that point.Therefore , the function is not differentiable at $x = (2n + 1)\dfrac{\pi }{2},n \in Z$.

Therefore the correct answer is option C.

Note: The continuity and differentiability of a function can be easily solved using the graph method but remember how to plot graphs of different functions . The polynomial functions are continuous and differentiable . Therefore , you can directly use them as such.