Solveeit Logo
Login

Question

Question: Let \(f\left( x \right) = \ln mx\,\left( {m > 0} \right)\) and \(g\left( x \right) = px.\) The equat...

Let f(x)=ln⁡mx (m>0)f\left( x \right) = \ln mx\,\left( {m > 0} \right) and g(x)=px.g\left( x \right) = px. The equation ∣f(x)∣=∣g(x)∣\left| {f\left( x \right)} \right| = \left| {g\left( x \right)} \right| has only one solution for
A). 0<p<me0 < p < \dfrac{m}{e}
B). p<mep < \dfrac{m}{e}
C). 0<p<em0 < p < \dfrac{e}{m}
D). p>mep > \dfrac{m}{e}

Explanation

Solution

Hint- For finding the solution of any equation we just draw the curve of both side of equation and then find the numbers of intersection which is the number of solution .Here in this case first of all we will draw the modulus of ln⁡(mx)\ln \left( {mx} \right) and then the curve of g(x)=px,g\left( x \right) = px, which is a straight line now if we want to have a single solution then the curve must intersect at only one point.

Complete step-by-step solution -
Since the curve must intersect at one point which means the line is tangent to the curve.
Let the coordinate of the point where line is tangent to the curve is P (h, k)
The slope of the curve at point P is given as
f(x)=ln⁡mx df(x)dx=dln⁡(mx)dx f′(x)=1mx×m=1x  f\left( x \right) = \ln mx \\\ \dfrac{{df\left( x \right)}}{{dx}} = \dfrac{{d\ln \left( {mx} \right)}}{{dx}} \\\ f'\left( x \right) = \dfrac{1}{{mx}} \times m = \dfrac{1}{x} \\\
Now substitute x = h in the above equation
f′(x)=1hf'\left( x \right) = \dfrac{1}{h}
Now we will write the equation of tangent at this point P
The equation of tangent is given by
y−k=1h(x−h)y - k = \dfrac{1}{h}\left( {x - h} \right)
For finding the values of P (h,k),\left( {h,k} \right), we will use the condition that the straight line passes through the origin it must satisfy the equation of the straight line
Substituting x = 0 and y = 0 in the straight line equation
⇒y−k=1h(x−h) ⇒0−k=1h(0−h) ⇒k=1  \Rightarrow y - k = \dfrac{1}{h}\left( {x - h} \right) \\\ \Rightarrow 0 - k = \dfrac{1}{h}\left( {0 - h} \right) \\\ \Rightarrow k = 1 \\\
Substituting the value of k = 1 in equation of the curve and x = h
f(x)=ln⁡mx k=ln⁡mh 1=ln⁡mh  f\left( x \right) = \ln mx \\\ k = \ln mh \\\ 1 = \ln mh \\\
Taking exponential both sides
h=emh = \dfrac{e}{m}
Therefore, the equation of the straight line becomes
y−k=1h(x−h)y - k = \dfrac{1}{h}\left( {x - h} \right)
Substituting the value of k and h
y−1=me(x−em) y=mxe  y - 1 = \dfrac{m}{e}\left( {x - \dfrac{e}{m}} \right) \\\ y = \dfrac{{mx}}{e} \\\

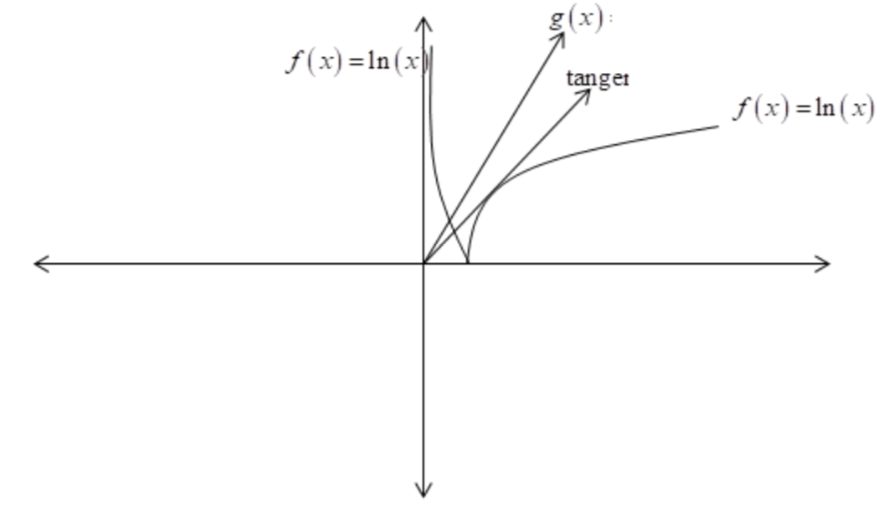
Now, from the figure it is clear that ∣f(x)∣=∣g(x)∣\left| {f\left( x \right)} \right| = \left| {g\left( x \right)} \right| will have only one solution when the slope of g(x)g\left( x \right) is greater than the slope of the line.
Hence, p>mep > \dfrac{m}{e}
Therefore, the correct option is D.

Note- In order to solve these types of questions, you need to learn about straight lines, their equations, parabolas, graphs of logarithmic function and how to find the tangent to any curve. In the above question we see that any line drawn from origin (here g(x)=px)\left( {here{\text{ }}g\left( x \right) = px} \right) must intersect the curve. So we have to find the condition that this line does not cut the curve at further points and so that our slope (p)\left( p \right) must be greater than that of tangent drawn at the exponential curve.