Question

Let f\left( x \right) = \left\\{ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\min \left\\{ {x,{x^2}} \right\\}}\\\\{{\rm{max}}\left\\{ {2x,{x^2} - 1} \right\\}}\end{array}}&{\begin{array}{*{20}{c}}{x \ge 0}\\\\{x < 0}\end{array}}\end{array}} \right. .
Then which of the following is not true?
A.$f\left( x \right)$ is continuous at $x = 0$
B.$f\left( x \right)$is not differentiable at $x = 1$
C.$f\left( x \right)$is not differentiable at exactly 3 points.
D.None of these.

Answer 1

We will first draw the required graph for the function. We will check its continuity and differentiability using the graph. Then we will find the doubtful points in the function.

Complete step-by-step answer:
We will find the solution using the graph of $f\left( x \right)$.
First, we will graph $x,{x^2}$ for $x \ge 0$ and $2x,{x^2} - 1$ for $x < 0$:

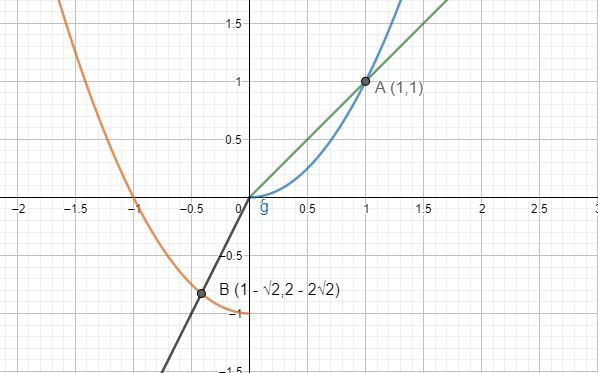
${x^2}$ is represented in blue, $x$ is represented in green, ${x^2} - 1$ is represented in red and $2x$ is represented in black.
We will find \min \left\\{ {x,{x^2}} \right\\}for $x \ge 0$. We can see from the graph that the blue curve is below the green line till $x = 1$. So \min \left\\{ {x,{x^2}} \right\\}is ${x^2}$ till $0 \le x < 1$ and $x$ for $x \ge 1 - \sqrt 2$.
We will find {\rm{max}}\left\\{ {2x,{x^2} - 1} \right\\}for $x < 0$. $x \ge 0$. We can see from the graph that the black line is above the red curve till $x = 1 - \sqrt 2$. So {\rm{max}}\left\\{ {2x,{x^2} - 1} \right\\}is $2x$ till $1 - \sqrt 2 < x < 0$ and ${x^2} - 1$ for $x \ge 1$.
We will draw the graph of $f\left( x \right)$ using this information:

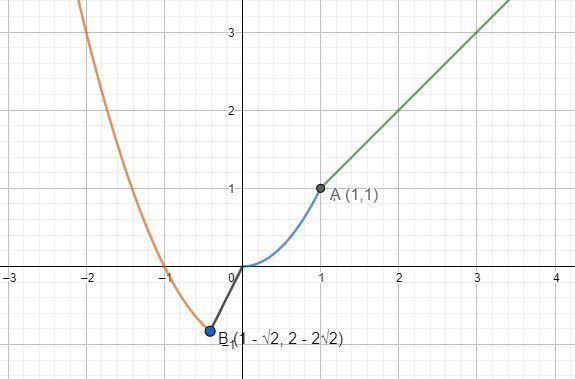
We know that a continuous function is a function whose graph can be drawn in one go without lifting the pen from the paper. We can see from the graph that $f\left( x \right)$ is a continuous function. So, $f\left( x \right)$ will also be continuous at $x = 1$. Option A is correct.
We know that a function is not differentiable at any of the corner points on its graph. We will identify the corner points in the graph of $f\left( x \right)$.
We can see that there are 3 corner points at $\left( {1 - \sqrt 2 ,2 - 2\sqrt 2 } \right)$, $\left( {0,0} \right)$ and $\left( {1,1} \right)$.
Options B and C are correct.
All the options are true.
We can conclude that the correct option is D – none of these.

Note: We can also find the solution without using the graphical method.
We will identify the points where we will need to check the continuity and differentiability. These points are those where the value of the piecewise function changes and 2 or more functions intersect. The points are:
$\left( {0,0} \right)$ - The value of the piecewise function changes here.
$\left( {1,1} \right)$ - Functions $x$ and ${x^2}$ intersect here.
$\left( {1 - \sqrt 2 ,2 - 2\sqrt 2 } \right)$ -Functions $2x$ and ${x^2} - 1$ intersect here.
We will check continuity of $f\left( x \right)$ at $x = 0$:
The left-hand limit will be $\mathop {\lim }\limits_{x \to {0^ - }} \left( {2x} \right) = 0$ and the right-hand limit will be $\mathop {\lim }\limits_{x \to {0^ + }} \left( x \right) = 0$. As ${\rm{L}}{\rm{.H}}{\rm{.L}}{\rm{.}} = {\rm{R}}{\rm{.H}}{\rm{.L}}{\rm{.}}$, $f\left( x \right)$is continuous at $x = 0$
We will check the differentiability of $f\left( x \right)$ at $x = 1$.
Right-hand derivative:
$\dfrac{d}{{dx}}\left( x \right)$ at $x = 1$
$\dfrac{d}{{dx}}\left( x \right) = 1 = {\rm{R}}{\rm{.H}}{\rm{.D}}.$
Left-hand derivative:
$\Rightarrow$ $\dfrac{d}{{dx}}\left( {{x^2}} \right)$ at $x = 1$
$\Rightarrow$ $\begin{array}{l}{\rm{ }}\dfrac{d}{{dx}}\left( {{x^2}} \right) = 2x\\\\{\dfrac{d}{{dx}}_{x = 1}}\left( {{x^2}} \right) = 2 \cdot 1\\\ \Rightarrow {\rm{ L}}{\rm{.H}}{\rm{.D}} = 2\end{array}$
As ${\rm{L}}{\rm{.H}}{\rm{.D}} \ne {\rm{R}}{\rm{.H}}{\rm{.D}}$, f(x) is not differentiable at $x = 1$.
We will check the differentiability of $f\left( x \right)$ at $x = 0$.
Left-hand derivative:
$\Rightarrow$ $\dfrac{d}{{dx}}\left( {2x} \right)$ at $x = 0$
\Rightarrow$$$\dfrac{d}{{dx}}\left( {2x} \right) = 2 = {\rm{L}}{\rm{.H}}{\rm{.D}}.$$ Right-hand derivative: \Rightarrow$$\dfrac{d}{{dx}}\left( {{x^2}} \right)$$ at $$x = 0$$ $$\begin{array}{l}{\rm{ }}\dfrac{d}{{dx}}\left( {{x^2}} \right) = 2x\\\\{\dfrac{d}{{dx}}_{x = 0}}\left( {{x^2}} \right) = 2 \cdot 0\\\ \Rightarrow {\rm{ R}}{\rm{.H}}{\rm{.D}} = 0\end{array}$$ As $${\rm{L}}{\rm{.H}}{\rm{.D}} \ne {\rm{R}}{\rm{.H}}{\rm{.D}}$$, therefore, f(x) is not differentiable at $$x = 0$$. We will now check the differentiability of $$f\left( x \right)$$ at $$x = 1 - \sqrt 2 $$. Left-hand derivative: $$\dfrac{d}{{dx}}\left( {{x^2} - 1} \right)$$ at $$x = 1 - \sqrt 2 $$ \Rightarrow$$\dfrac{d}{{dx}}\left( {2x} \right) = 2 = {\rm{L}}{\rm{.H}}{\rm{.D}}.$$ Right-hand derivative: \Rightarrow$$\dfrac{d}{{dx}}\left( {2x} \right)$$ at $$x = 1 - \sqrt 2 $$ \Rightarrow$ ${\rm{ }}\dfrac{d}{{dx}}\left( {2x} \right) = 2 = {\rm{R}}{\rm{.H}}{\rm{.D}}$
As ${\rm{L}}{\rm{.H}}{\rm{.D}} \ne {\rm{R}}{\rm{.H}}{\rm{.D}}$, therefore f(x) is not differentiable at$x = 1 - \sqrt 2$.
$\therefore$ Options B and C are also not incorrect.
We can conclude that the correct answer is option D – none of these.