Question

Let $f\left( n \right)$ be the number of regions in which n coplanar circles can divide the plane. If it is known that each pair of circles intersect in two different point and no three of them have common point of intersection, then
(a). $f\left( 20 \right)=382$
(b). $f\left( n \right)$ is always an even number
(c). ${{f}^{-1}}\left( n \right)=10$
(d). $f\left( n \right)$ can be odd

Answer 1

Hint: We can see clearly that we will have to check each option one by one. But, in this question, the problem is that we cannot draw 20 circles and check the number of regions because it is practically impossible. So, we are going to obtain a function of n (the number of circles). After obtaining the function, we will put the value of ‘n’ in the function and we will get the answer. So, let us proceed to solve the question.

Complete step-by-step answer:
Let us check, what will be the number of region if we take only one circle in a plane: -

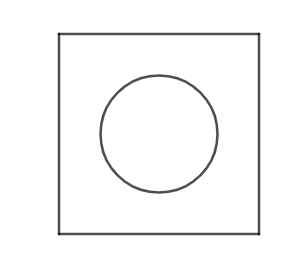
We can see that one circle divides the plane with two regions. So, $f\left( 1 \right)=2$. Now, let us check what will happen if we take two circles.

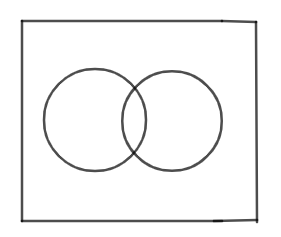
Thus, the total number of regions obtained are 4. One region is the outer region, one region is the region between the intersection of two circles and the other two regions are the regions of individual circles. So, we can say that $f\left( 2 \right)=4$ . Now, let us check how many regions we will get if we take three circles in a plane.

Here, we get the total number of regions as 8. So, in this case we can say that $f\left( 3 \right)=8$ . Now, let us take one more case in which the number of intersecting circles is 4. So, let us see what is the number of regions obtained.

In this case, we get a total 14 regions. So, in this case, we can say that $f\left( 4 \right)=14$ . Now, we have enough values of function $f\left( n \right)$ to generate our own function $f\left( n \right)$ . We can see the pattern of n as: -
$f\left( 1 \right),f\left( 2 \right),f\left( 3 \right),f\left( 4 \right),.....\Rightarrow 2,4,8,14....$
The difference $f\left( 2 \right)-f\left( 1 \right)=4-2=2$
The difference $f\left( 3 \right)-f\left( 2 \right)=8-4=4$
The difference $f\left( 4 \right)-f\left( 3 \right)=14-8=6$
We can see that these differences are in A.P. So, the function $f\left( n \right)$ will be quadratic. Let this function $f\left( n \right)=a{{n}^{2}}+bn+c$. Now, with the help of $f\left( 1 \right),f\left( 2 \right),f\left( 3 \right),f\left( 4 \right),$ we will find the values of a, b and c. So, let us solve
$f\left( 1 \right)=a{{\left( 1 \right)}^{2}}+b\left( 1 \right)+c$
$\Rightarrow a+b+c=2$ ………………………………(i)
$f\left( 2 \right)=a{{\left( 2 \right)}^{2}}+b\left( 2 \right)+c$
$\Rightarrow 4a+2b+c=4$ ………………………..(ii)
$f\left( 3 \right)=a{{\left( 3 \right)}^{2}}+b\left( 3 \right)+c$
$\Rightarrow 9a+3b+c=8$ …………………………….(iii)
Now, we subtract (ii) from (iii). After subtracting we get: -
$5a+b=4$ …………………………..(iv)
Now, we subtract (i) from (ii). After subtracting we get: -
$3a+b=2$ …………………………..(v)
Now, we subtract (iv) from (v). After subtracting we get: -
$2a=2$
$\Rightarrow a=1$
Now, we will put $a=1$ in equation (v) to get the value of b. After putting this, we get: -
$3\left( 1 \right)+b=2$
$\Rightarrow b=-1$
Now, we will put the values of a and b in (i). After putting we get: -
$1-1+c=2$
$\Rightarrow c=2$
So, now we have the values of a, b and c. So, the required function $f\left( n \right)$ will be: -
$f\left( n \right)={{n}^{2}}-n+2$
Now, we are going to check each option one by one.
Option (a): - $f\left( 20 \right)={{\left( 20 \right)}^{2}}-20+2=400-20+2=382$
Therefore, $f\left( 20 \right)=382$
Option (b): - Let us check the nature of $f\left( n \right)$ at the integer values
$f\left( n \right)={{n}^{2}}-n+2$
$=n\left( n-1 \right)+2$
$n\left( n-1 \right)$ is an even number and 2 is an even number, so $f\left( n \right)$ will always be even.
Option (c): - In option (c), we have to find the value of $f\left( 10 \right)$ . $f\left( 10 \right)={{\left( 10 \right)}^{2}}-\left( 10 \right)+2=32$
Option (d): - $f\left( n \right)$ will always be even.
Hence, (a), (b) and (c) are correct.

Note: We must assume that the function formed is a quadratic in n. This is because the difference between the consecutive terms form an A.P. and this difference is the first difference. This can be explained as follows: - Any series whose ${{r}^{th}}$ difference is in AP then the general term of the series is ${{a}_{1}}{{n}^{r+1}}+{{a}_{2}}{{n}^{r}}+{{a}_{3}}{{n}^{r-1}}.....{{a}_{r+1}}n+{{a}_{r+2}}$ . In the above series, when we put the value of $r=1$ (because we have the first difference as AP), we get a quadratic equation.