Solveeit Logo
Login

Question

Question: Let \[f:\left[ { - \dfrac{1}{2},2} \right] \to R\] and \(g:\left[ { - \dfrac{1}{2},2} \right] \to R\...

Let f:[−12,2]→Rf:\left[ { - \dfrac{1}{2},2} \right] \to R and g:[−12,2]→Rg:\left[ { - \dfrac{1}{2},2} \right] \to R be function defined by f(x)=[x2−3]f(x) = \left[ {{x^{^2}} - 3} \right] and g(x)=∣x∣f(x)+∣4x−7∣f(x),g(x) = \left| x \right|f(x) + \left| {4x - 7} \right|f(x), where []\left[ {} \right]denotes the greatest integer less than or equal to y∈Ry \in R. Then
(A) ff is discontinuous at three point in [−12,2]\left[ { - \dfrac{1}{2},2} \right]
(B) ff is discontinuous at four point in [−12,2]\left[ { - \dfrac{1}{2},2} \right]
(C) gg is NOT differentiable exactly at four point in (−12,2)\left( { - \dfrac{1}{2},2} \right)
(D) gg is NOT differentiable exactly at five point in (−12,2)\left( { - \dfrac{1}{2},2} \right)

Explanation

Solution

First we find point of discontinuity of f(x)=[x2−3]f(x) = \left[ {{x^{^2}} - 3} \right] by making graph. As we see that given function is a greatest integer function so it define only at integer point.
Next from the point of discontinuity of f(x)f(x) we define the function g(x)=∣x∣f(x)+∣4x−7∣f(x),g(x) = \left| x \right|f(x) + \left| {4x - 7} \right|f(x),
And find a point where it is not differentiable.

Complete step by step answer:
Given f(x)=[x2−3]f(x) = \left[ {{x^{^2}} - 3} \right] is a greatest integer function and define in −12⩽x⩽2 - \dfrac{1}{2} \leqslant x \leqslant 2
Now we find x2−3{x^2} - 3 is define where
from the value of xx
we say that 0⩽x2⩽40 \leqslant {x^2} \leqslant 4
now subtract 3 from above given equation
⇒−3⩽x2−3⩽1\Rightarrow - 3 \leqslant {x^2} - 3 \leqslant 1
Now take a greatest integer
⇒−3⩽[x2−3]⩽1\Rightarrow - 3 \leqslant [{x^2} - 3] \leqslant 1
From this we can say f(x)f(x) take value from [−3,1]\left[ { - 3,1} \right] only at integer value.
f(x)=−3,,−2,−1,0,1f(x) = \\{ - 3,, - 2, - 1,0,1\\}
Now
1.f(x)=−3f(x) = - 3
Then [x2−3]=−3\left[ {{x^2} - 3} \right] = - 3
So −3⩽x2−3⩽−2 - 3 \leqslant {x^2} - 3 \leqslant - 2
⇒0⩽x2⩽1\Rightarrow 0 \leqslant {x^2} \leqslant 1
From here −1⩽x⩽1 - 1 \leqslant x \leqslant 1
2. f(x)=−2f(x) = - 2
Then [x2−3]=−2\left[ {{x^2} - 3} \right] = - 2
So −2⩽x2−3⩽−1 - 2 \leqslant {x^2} - 3 \leqslant - 1
⇒1⩽x2⩽2\Rightarrow 1 \leqslant {x^2} \leqslant 2
Now we take square root to find xx
From here 1⩽x⩽21 \leqslant x \leqslant \sqrt 2
3. f(x)=−1f(x) = - 1
Then [x2−3]=−1\left[ {{x^2} - 3} \right] = - 1
So −1⩽x2−3⩽0 - 1 \leqslant {x^2} - 3 \leqslant 0
⇒2⩽x2⩽3\Rightarrow 2 \leqslant {x^2} \leqslant 3
Now we take square root to find xx
From here 2⩽x⩽3\sqrt 2 \leqslant x \leqslant \sqrt 3
4. f(x)=0f(x) = 0
Then [x2−3]=0\left[ {{x^2} - 3} \right] = 0
So 0⩽x2−3⩽10 \leqslant {x^2} - 3 \leqslant 1
⇒3⩽x2⩽4\Rightarrow 3 \leqslant {x^2} \leqslant 4
Now we take square root to find xx
From here 3⩽x⩽2\sqrt 3 \leqslant x \leqslant 2
5f(x)=1f(x) = 1
Then [x2−3]=1\left[ {{x^2} - 3} \right] = 1
So 1⩽x2−3⩽21 \leqslant {x^2} - 3 \leqslant 2
⇒4⩽x2⩽5\Rightarrow 4 \leqslant {x^2} \leqslant 5

Now we take the square root to find xx
From here 2⩽x⩽52 \leqslant x \leqslant \sqrt 5 but we know that function can not take value more than 2
So x=2x = 2

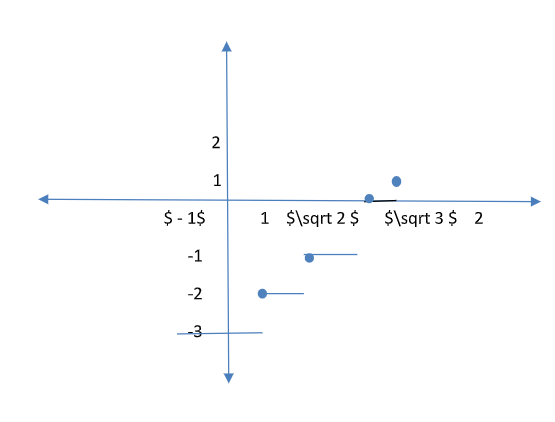
So from this, we can say it is discontinuous at 4 points.
Point of discontinuity \left\\{ {1,\sqrt 2 ,\sqrt 3 ,2,} \right\\}
So option B is the correct answer.
Now for function g(x)=∣x∣f(x)+∣4x−7∣f(x),g(x) = \left| x \right|f(x) + \left| {4x - 7} \right|f(x),
By putting value of f(x)f(x)
So first when −1⩽x<1 - 1 \leqslant x < 1 here f(x)=−3f(x) = - 3
So g(x)=−3∣x∣−3∣4x−7∣g(x) = - 3\left| x \right| - 3\left| {4x - 7} \right|
When −1⩽x<0 - 1 \leqslant x < 0 then g(x)=3x+3(4x−7)g(x) = 3x + 3\left( {4x - 7} \right)
g(x)=15x−21g(x) = 15x - 21
And when 0⩽x<10 \leqslant x < 1
In this ∣4x−7∣\left| {4x - 7} \right| open with negative sign
So g(x)=−3x+3(4x−7)g(x) = - 3x + 3\left( {4x - 7} \right)
g(x)=9x−21g(x) = 9x - 21

2. when 1⩽x<21 \leqslant x < \sqrt 2 ; f(x)=−2f(x) = - 2
So g(x)=−2∣x∣−2∣4x−7∣g(x) = - 2\left| x \right| - 2\left| {4x - 7} \right|
In this ∣4x−7∣\left| {4x - 7} \right| open with negative sign
so g(x)=−2x+2(4x−7)g(x) = - 2x + 2\left( {4x - 7} \right)
g(x)=6x−14g(x) = 6x - 14

3. when 2⩽x<3\sqrt 2 \leqslant x < \sqrt 3 ; f(x)=−1f(x) = - 1
So g(x)=−∣x∣−∣4x+7∣g(x) = - \left| x \right| - \left| {4x + 7} \right|
In this ∣4x−7∣\left| {4x - 7} \right| open with negative sign
so g(x)=3x−7g(x) = 3x - 7

4. When 3⩽x<2\sqrt 3 \leqslant x < 2; f(x)=0f(x) = 0
So g(x)=0g(x) = 0.

5. when x=2;f(x)=1x = 2;f(x) = 1
So g(x)=∣x∣+∣4x−7∣g(x) = \left| x \right| + \left| {4x - 7} \right|
g(x)=5x−7g(x) = 5x - 7
Now we have to find differentiability of g(x)g(x)
(i) At x=0x = 0
Right hand derivative g′(a+)=lim⁡h→0f(a+h)−f(a)hg'(a + ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{f(a + h) - f(a)}}{h}
So g′(0+)=lim⁡h→0f(0+h)−f(0)hg'(0 + ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{f(0 + h) - f(0)}}{h}
g′(0+)=lim⁡h→09h−21+21hg'(0 + ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{9h - 21 + 21}}{h}
So g′(0+)=lim⁡h→09hh=9g'(0 + ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{9h}}{h} = 9.
So right hand derivative = 9
Now left hand derivative
g′(a−)=lim⁡h→0f(a−h)−f(a)−hg'(a - ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{f(a - h) - f(a)}}{{ - h}}
So g′(0−)=lim⁡h→0f(0−h)−f(0)−hg'(0 - ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{f(0 - h) - f(0)}}{{ - h}}
g′(0−)=lim⁡h→015h−21+21−hg'(0 - ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{15h - 21 + 21}}{{ - h}}
g′(0−)=lim⁡h→015h−h=−15g'(0 - ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{15h}}{{ - h}} = - 15
So left hand limit is not equal to right hand limit so function g(x)g(x) is not deprivable at x=0x = 0
(ii). At x=1x = 1
Left hand derivative
g′(1−)=lim⁡h→0f(1−h)−f(1)−hg'(1 - ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{f(1 - h) - f(1)}}{{ - h}}
g′(1−)=lim⁡h→09(1−h)−21−6+14−hg'(1 - ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{9\left( {1 - h} \right) - 21 - 6 + 14}}{{ - h}}
g′(1−)=lim⁡h→0−9h−4−hg'(1 - ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{ - 9h - 4}}{{ - h}}
By using L’HOSPITAL RULE
g′(1−)=lim⁡h→0−9−1=9g'(1 - ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{ - 9}}{{ - 1}} = 9
And right hand limit.
g′(1+)=lim⁡h→0f(1+h)−f(1)h=lim⁡h→o6−6h−14−6+14−h=6g'(1 + ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{f(1 + h) - f(1)}}{h} = \mathop {\lim }\limits_{h \to o} \dfrac{{6 - 6h - 14 - 6 + 14}}{{ - h}} = 6
So left and write hand derivative are different so at x=1x = 1 it is not derivative
So by definition we can say if f(x)f(x) is not continuous and g(x)g(x)is a function of f(x)f(x) in this case g(x)g(x) is also discontinuous at these points. And if a function is not continuous at any point so the function is not derivable at these point
So 2,3\sqrt 2 ,\sqrt 3 are point of discontinuity of g(x)g(x) that mean it is not derivable at these point also
We know that f(x)f(x) is discontinuous at x=2x = 2 but we can not include because queation ask point of not differentiability in between (−12,2)\left( { - \dfrac{1}{2},2} \right)
So gg is NOT differentiable exactly at four point in (−12,2)\left( { - \dfrac{1}{2},2} \right)
Point where g(x)g(x) is not differentiable is
x=0,1,2,3x = \\{ 0,1,\sqrt 2 ,\sqrt 3 \\}

Therefore, option (B) and (C) are correct.

Note:
The differentiability of a function can be found by making a graph.
And differentiability of a function at the boundary point can be found by using one hand derivative either left or right hand.