Solveeit Logo
Login

Question

Question: Let \(f:\left[ {0,4\pi } \right] \to \left[ {0,\pi } \right]\) be defined by \(f\left( x \right) = {...

Let f:[0,4π]→[0,π]f:\left[ {0,4\pi } \right] \to \left[ {0,\pi } \right] be defined by f(x)=cos⁡−1(cos⁡x)f\left( x \right) = {\cos ^{ - 1}}\left( {\cos x} \right) . The number of points x∈[0,4π]x \in \left[ {0,4\pi } \right] satisfying the equation f(x)=10−x10f\left( x \right) = \dfrac{{10 - x}}{{10}} is.

Explanation

Solution

The number of points of satisfaction is the points of intersection between the two given functions.
Try to draw the graph of both given functions and graphically find the point of intersection.
Intersection points are the points where the graph of both given functions cut each other.
The slope of a straight line Ax+By+C=0Ax + By + C = 0, is given by the derivative of the equation of the line with respect to x.
For the function f(x):x→yf\left( x \right):x \to y, the domain of the function is the set of all possible values of xx for which the function is defined. The range of the function is the set of all output values of the function at xx.

Complete step-by-step answer:
Step 1: Draw a graph of f(x)=cos⁡−1(cos⁡x)f\left( x \right) = {\cos ^{ - 1}}\left( {\cos x} \right)
To draw the graph of f(x)=cos⁡−1(cos⁡x)f\left( x \right) = {\cos ^{ - 1}}\left( {\cos x} \right) , we will use both the functions cos⁡x\cos x and cos⁡−1x{\cos ^{ - 1}}x.
Let us consider the graph of the trigonometric function f(x)=cos⁡xf\left( x \right) = \cos x
Let y=f(x)y = f\left( x \right)

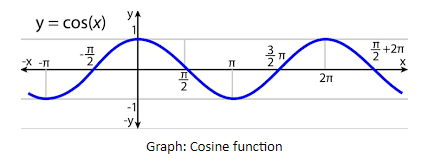
The function cos⁡x\cos x is defined on all the real values of the xx. Thus,
Domain: R\mathbb{R} , where R\mathbb{R} is the set of real numbers.
The maximum output value of the function cos⁡x\cos x is +1 and the minimum output value is -1, and all other values of cos⁡x\cos x lie between +1 and -1. Thus,
Range: [−1,1]\left[ { - 1,1} \right]
Now, let us consider the graph of the inverse trigonometric function f(x)=cos⁡−1xf\left( x \right) = {\cos ^{ - 1}}x :

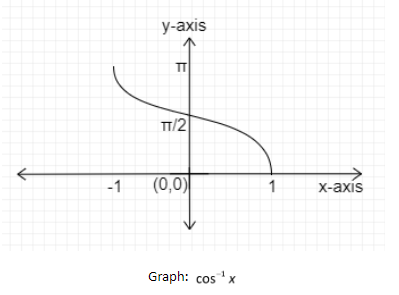
It is taking the values from +1 to -1. So, Domain = [−1,1]\left[ { - 1,1} \right]
The output values of the function are from 0 to π\pi . So, Range = [0,π]\left[ {0,\pi } \right]

Now draw the Graph of f(x)=cos⁡−1(cos⁡x)f\left( x \right) = {\cos ^{ - 1}}\left( {\cos x} \right)
Given that the function is defined for f:[0,4π]→[0,π]f:\left[ {0,4\pi } \right] \to \left[ {0,\pi } \right]
For the interval x∈[0,π]x \in \left[ {0,\pi } \right]
From the above graph of the function f(x)=cos⁡xf\left( x \right) = \cos x , the output values for the interval [0,π]\left[ {0,\pi } \right] is between -1 and +1. The output value ofcos⁡x\cos x is the input value of cos⁡−1x{\cos ^{ - 1}}x .
And from the above graph of the function f(x)=cos⁡−1xf\left( x \right) = {\cos ^{ - 1}}x , the output values for the interval [−1,+1]\left[ { - 1, + 1} \right] is 0 to π\pi . Thus,
f(x)=cos⁡−1(cos⁡x)=xf\left( x \right) = {\cos ^{ - 1}}\left( {\cos x} \right) = x
⇒f(x)=x\Rightarrow f\left( x \right) = x
( Let y=f(x)y = f\left( x \right)
Differentiation dydx\dfrac{{dy}}{{dx}} gives the slope of the function.
i.e. y=xy = x, a straight line with slope dydx=1\dfrac{{dy}}{{dx}} = 1)
The range for the interval x∈[0,π]x \in \left[ {0,\pi } \right] is f(x)∈[0,π]f\left( x \right) \in \left[ {0,\pi } \right]
Thus the graph of f(x)=cos⁡−1(cos⁡x)f\left( x \right) = {\cos ^{ - 1}}\left( {\cos x} \right) in the interval x∈[0,π]x \in \left[ {0,\pi } \right] is a straight line with slope 1.

For the interval x∈[π,2π]x \in \left[ {\pi ,2\pi } \right]
From the above graph of the function f(x)=cos⁡xf\left( x \right) = \cos x , the output values for the interval [π,2π]\left[ {\pi ,2\pi } \right] is between -1 and 0.
In f(x)=cos⁡−1(cos⁡x)f\left( x \right) = {\cos ^{ - 1}}\left( {\cos x} \right) , the domain is the range of cos⁡x\cos x , but for the domain∈[−1,0] \in \left[ { - 1,0} \right] , the function cos⁡−1x{\cos ^{ - 1}}x is not defined.
Therefore, using the property of the cosine function cos⁡x=cos⁡(2π−x)\cos x = \cos \left( {2\pi - x} \right)
f(x)=cos⁡−1(cos⁡x)f\left( x \right) = {\cos ^{ - 1}}\left( {\cos x} \right)
Therefore, f(x)=cos⁡−1(cos⁡(2π−x))=2π−xf\left( x \right) = {\cos ^{ - 1}}\left( {\cos \left( {2\pi - x} \right)} \right) = 2\pi - x
⇒f(x)=2π−x\Rightarrow f\left( x \right) = 2\pi - x
(Let y=f(x)y = f\left( x \right)
Differentiation dydx\dfrac{{dy}}{{dx}} gives the slope of the function.
i.e. y=2π−xy = 2\pi - x, a straight line with slope dydx=−1\dfrac{{dy}}{{dx}} = - 1)
For x=π,x = \pi ,
f(x)=2π−π=πf\left( x \right) = 2\pi - \pi = \pi
For x=2π,x = 2\pi ,
f(x)=2π−2π=0f\left( x \right) = 2\pi - 2\pi = 0
The range for the interval x∈[π,2π]x \in \left[ {\pi ,2\pi } \right] is f(x)∈[0,π]f\left( x \right) \in \left[ {0,\pi } \right]
Thus the graph of f(x)=cos⁡−1(cos⁡x)f\left( x \right) = {\cos ^{ - 1}}\left( {\cos x} \right) in the interval x∈[π,2π]x \in \left[ {\pi ,2\pi } \right] is a straight line with slope -1.
Therefore, the drawn graph of f(x)=cos⁡−1(cos⁡x)f\left( x \right) = {\cos ^{ - 1}}\left( {\cos x} \right) is the following:

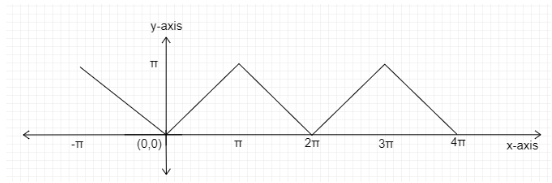
Graph: f(x)=cos⁡−1(cos⁡x)f\left( x \right) = {\cos ^{ - 1}}\left( {\cos x} \right)
Step 2: Draw graph of f(x)=10−x10f\left( x \right) = \dfrac{{10 - x}}{{10}}
We have drawn the graph of one given function. Now let’s draw the function of other given functions to find the intersection points between them.
f(x)=1−x10f\left( x \right) = 1 - \dfrac{x}{{10}}

xx001010
yy1100

Point 10≃3π10 \simeq 3\pi
Let y=f(x)y = f\left( x \right)
Differentiation dydx\dfrac{{dy}}{{dx}} gives the slope of the function. Thus,
The slope of the line f(x)=1−x10f\left( x \right) = 1 - \dfrac{x}{{10}}, is dydx=−1\dfrac{{dy}}{{dx}} = - 1
Therefore, the drawn graph f(x)=10−x10f\left( x \right) = \dfrac{{10 - x}}{{10}} is the following:

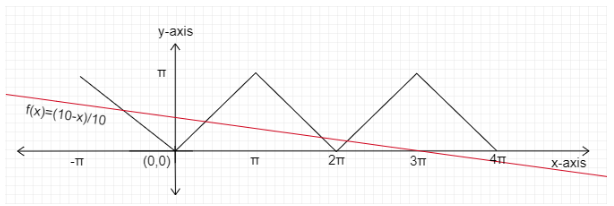
Graph: f(x)=10−x10f\left( x \right) = \dfrac{{10 - x}}{{10}}
Step 3: Count the point of intersection from the graph:
For x∈[0,4π]x \in \left[ {0,4\pi } \right]
Function f(x)=cos⁡−1(cos⁡x)f\left( x \right) = {\cos ^{ - 1}}\left( {\cos x} \right) and f(x)=10−x10f\left( x \right) = \dfrac{{10 - x}}{{10}} intersects each other 3 points shown as below:

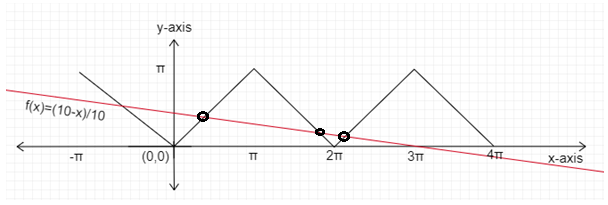
Final answer: At 3 points function f(x)=cos⁡−1(cos⁡x)f\left( x \right) = {\cos ^{ - 1}}\left( {\cos x} \right) satisfies f(x)=10−x10f\left( x \right) = \dfrac{{10 - x}}{{10}} in the interval x∈[0,4π]x \in \left[ {0,4\pi } \right]

Note: Following graphs will be useful in future reference.
Graph of the sine function.

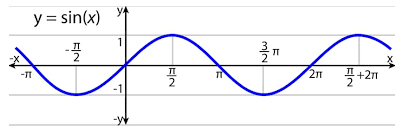
The function sin⁡x\sin x is defined on all the real values of the xx. Thus,
Domain: R\mathbb{R} , where R\mathbb{R} is the set of real numbers.
The maximum output value of the function sin⁡x\sin x is +1 and the minimum output value is -1, and all other values of sin⁡x\sin x lie between +1 and -1. Thus,
Range: [−1,1]\left[ { - 1,1} \right]
The graph of sin⁡x\sin x and cos⁡x\cos x is shifted by π2\dfrac{\pi }{2}. Thus, we can also interchange between sine and cosine function as well by using the relation: sin⁡x=cos⁡(π2−x)\sin x = \cos \left( {\dfrac{\pi }{2} - x} \right) or cos⁡x=sin⁡(π2−x)\cos x = \sin \left( {\dfrac{\pi }{2} - x} \right) .
Graph of sine inverse function.

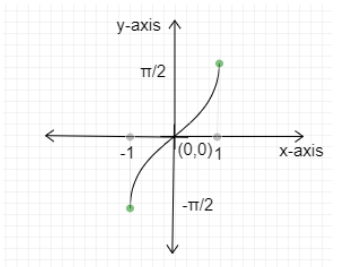
It is taking the values from +1 to -1. So, Domain = [−1,1]\left[ { - 1,1} \right]
The output values of the function are from −π2 - \dfrac{\pi }{2} to π2\dfrac{\pi }{2}. So, Range = [−π2,π2]\left[ { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right]