Question

Let $f:\left[ 0,\infty \right)\to R$ be a continuous function such that $f\left( x \right)=1-2x+\int\limits_{0}^{x}{{{e}^{x-t}}f\left( t \right)dt}$
for all $x\in \left[ 0,\infty \right)$ .Then which of the following statement(s) is(are) TRUE?
(a) The curve $y=f\left( x \right)$ passes through the point $\left( 1,2 \right)$ .
(b) The curve $y=f\left( x \right)$ passes through the point $\left( 2,-1 \right)$
(c) The area of the region \left\\{ \left( x,y \right)\in \left[ 0,1 \right]\times R:f\left( x \right)\le y\le \sqrt{1-{{x}^{2}}} \right\\} is $\dfrac{\pi -2}{4}$ .
(d) The area of the region \left\\{ \left( x,y \right)\in \left[ 0,1 \right]\times R:f\left( x \right)\le y\le \sqrt{1-{{x}^{2}}} \right\\}is $\dfrac{\pi -1}{4}$

Answer 1

We will first convert the given function involving integration , into a differential equation so that we can have a simple functional value in term of $x$ . Once we have a function, we can check the first 2 options (a) and (b) , if the points lie on the function or not. Also when we have the region lying between 2 curves, we can use the method of integration to find the area.

Complete step-by-step answer:
Consider the given function,
$f\left( x \right)=1-2x+\int\limits_{0}^{x}{{{e}^{x-t}}f\left( t \right)dt}$
Now, since the integration is with respect to $t$ and $x$ is independent of $t$ , therefore ${{e}^{x}}$ can be taken out of the integration, i.e.
$f\left( x \right)=1-2x+{{e}^{x}}\int\limits_{0}^{x}{{{e}^{-t}}f\left( t \right)dt}$
On multiplying both the sides by ${{e}^{-x}}$ ,we get,
${{e}^{-x}}f\left( x \right)={{e}^{-x}}-2x{{e}^{-x}}+\int\limits_{0}^{x}{{{e}^{-t}}f\left( t \right)dt}$
Now, we will differentiate both the sides of the equation, and so that it becomes a differential equation and further solve it,
$\begin{aligned} & -{{e}^{-x}}f\left( x \right)+{{e}^{-x}}f'\left( x \right)=-{{e}^{-x}}\left( 1-2x \right)+{{e}^{-x}}\left( -2 \right)+{{e}^{-t}}f\left( t \right)|_{0}^{x} \\\ & \Rightarrow -{{e}^{-x}}f\left( x \right)+{{e}^{-x}}f'\left( x \right)=-{{e}^{-x}}\left( 1-2x \right)-2{{e}^{-x}}+{{e}^{-x}}f\left( x \right) \\\ & \Rightarrow -f\left( x \right)+f'\left( x \right)=-\left( 1-2x \right)-2+f\left( x \right) \\\ & \Rightarrow f'\left( x \right)-2f\left( x \right)=2x-3 \\\ \end{aligned}$
Now, we have got a non homogeneous first order linear differential equation which can easily solved for $f\left( x \right)$
The integrating factor for this differential equation is
$\begin{aligned} & {{e}^{\int{-2dx}}} \\\ & ={{e}^{-2x}} \\\ \end{aligned}$
Now, multiplying the differential equation with ${{e}^{-2x}}$ on both the sides, we get,
${{e}^{-2x}}f'\left( x \right)-2{{e}^{-2x}}f\left( x \right)=\left( 2x-3 \right){{e}^{-2x}}$
Now, notice the Right Hand Side, it is the differentiation of a function i.e. $\dfrac{d}{dx}\left( {{e}^{-2x}}f\left( x \right) \right)$ So, now the equation has become,
$\dfrac{d}{dx}\left( {{e}^{-2x}}f\left( x \right) \right)=\left( 2x-3 \right){{e}^{-2x}}$
Now, integrating both the sides with respect to $''x''$ ,we get,
${{e}^{-2x}}f\left( x \right)=\int{\left( 2x-3 \right){{e}^{-2x}}dx}$
Now, using integration by parts for solving Right Hand Side,
$\begin{aligned} & {{e}^{-2x}}f\left( x \right)=\left( 2x-3 \right)\int{{{e}^{-2x}}dx}-\int{\left( 2\int{{{e}^{-2x}}dx} \right)dx} \\\ & =\left( 2x-3 \right)\dfrac{{{e}^{-2x}}}{-2}-\dfrac{{{e}^{-2x}}}{2}+C \\\ & \Rightarrow f\left( x \right)=-\dfrac{\left( 2x-3 \right)}{2}-\dfrac{1}{2}+C{{e}^{2x}} \end{aligned}$
Now, if we see the given function in the start, where integration was involved
$f\left( x \right)=1-2x+\int\limits_{0}^{x}{{{e}^{x-t}}f\left( t \right)dt}$
If we put $x=0$ , we get
$\begin{aligned} & f\left( 0 \right)=1-2.0+\int\limits_{0}^{0}{{{e}^{x-t}}f\left( t \right)dt} \\\ & \Rightarrow f\left( 0 \right)=1 \\\ \end{aligned}$
Putting this relation , on our solution we get the value of $C$
$\begin{aligned} & 1=-\dfrac{\left( 2.0-3 \right)}{2}-\dfrac{1}{2}+C{{e}^{2.0}} \\\ & 1=1+C \\\ & C=0 \\\ \end{aligned}$
Now, the solution is,
$\begin{aligned} & f\left( x \right)=-\dfrac{\left( 2x-3 \right)}{2}-\dfrac{1}{2} \\\ & f\left( x \right)=1-x \\\ \end{aligned}$
Now, we have the function and we have to check of the option(s) is(are) correct
So, we will check every option one by one
For (a)
We have to check if $\left( 1,2 \right)$ passes through the line or satisfies the function $f\left( x \right)=1-x$
Put, $x=1$
$\begin{aligned} & f\left( 1 \right)=1-1 \\\ & =0\ne 2 \end{aligned}$
Hence, option (a) is not correct.
For (b)
We have to check if $\left( 2,-1 \right)$ passes through the line or satisfies the function $f\left( x \right)=1-x$
Put, $x=2$
$\begin{aligned} & f\left( 2 \right)=1-2 \\\ & =-1 \end{aligned}$
Hence, option (b) is correct.
For (c) and (d)
We have to check the area of region \left\\{ \left( x,y \right)\in \left[ 0,1 \right]\times R:1-x\le y\le \sqrt{1-{{x}^{2}}} \right\\}

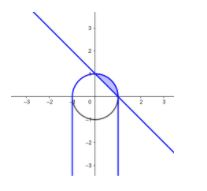
So we have to find the area of the shaded region,
Area = $\begin{aligned} & \int\limits_{0}^{1}{\left( \sqrt{1-{{x}^{2}}}-\left( 1-x \right) \right)dx} \\\ & =\dfrac{x}{2}\sqrt{1-{{x}^{2}}}+\dfrac{1}{2}{{\operatorname{Sin}}^{-1}}x|_{0}^{1}-\dfrac{1}{2}{{\left( 1-x \right)}^{2}}|_{0}^{1} \\\ & =\dfrac{1}{2}\dfrac{\pi }{2}-\dfrac{1}{2} \\\ & =\dfrac{\pi -2}{4} \\\ \end{aligned}$
Hence, option (c) is correct.

So, the correct answers are “Option (b) and (c)”.

Note: Note that for finding the shaded region of which we have to find the area , we first plot both the curves involved in the region. Then take the first inequality $1-x\le y$
We have 2 options to take the region at the right or the left of the line. So, to clear that confusion you can take a point from a particular region and then if that point satisfies this inequality then that particular region should be considered , if not then take the other region. Similarly, we can find the region from the second inequality. And the common region of both inequality , is the region whose area we have to evaluate.