Question

Let f, g are two continuous and twice derivable functions such that f(0) = f(3) = 0; f(1).f(2) < 0; g(0) = g(3) = 0. Number of roots of equation f"(x).g(x) + f'(x).g'(x) = 0 in (-1,5) cannot be

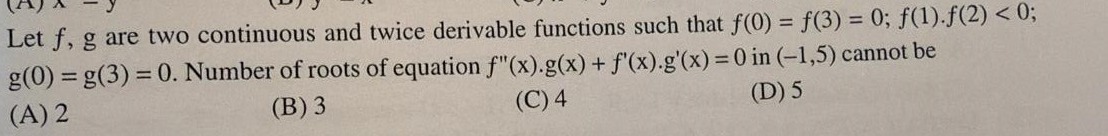
• A. 2
• B. 3
• C. 4
• D. 5

Answer 1

Answer: (A)

2

Answer 2

Let the given equation be $f''(x)g(x) + f'(x)g'(x) = 0$.

This equation is the derivative of the product $h(x) = f'(x)g(x)$. So the equation is $h'(x) = 0$. We need to find the number of roots of $h'(x) = 0$ in the interval $(-1, 5)$.

We are given that $f$ and $g$ are continuous and twice derivable functions. We are given $f(0) = 0$ and $f(3) = 0$. We are also given $g(0) = 0$ and $g(3) = 0$.

Let's evaluate $h(x) = f'(x)g(x)$ at $x=0$ and $x=3$. $h(0) = f'(0)g(0) = f'(0) \times 0 = 0$. $h(3) = f'(3)g(3) = f'(3) \times 0 = 0$.

Since $h(x)$ is continuous in $[0, 3]$ (as $f'$ and $g$ are continuous) and derivable in $(0, 3)$, and $h(0) = h(3) = 0$, by Rolle's Theorem, there exists at least one root of $h'(x) = 0$ in the interval $(0, 3)$.

Now consider the condition $f(1)f(2) < 0$. This means $f(1)$ and $f(2)$ have opposite signs. Since $f$ is continuous, by the Intermediate Value Theorem, there exists at least one root of $f(x) = 0$ in the interval $(1, 2)$. Let's call this root $r_0$, so $f(r_0) = 0$ for some $r_0 \in (1, 2)$.

Now we have three known roots of $f(x) = 0$: $0$, $r_0 \in (1, 2)$, and $3$. Since $f$ is continuous and derivable, we can apply Rolle's Theorem to $f(x)$ on the intervals $[0, r_0]$ and $[r_0, 3]$.

• In $[0, r_0]$, since $f(0) = f(r_0) = 0$, there exists at least one root of $f'(x) = 0$ in $(0, r_0)$. Let's call it $r_1$. So $f'(r_1) = 0$ for some $r_1 \in (0, r_0)$.
• In $[r_0, 3]$, since $f(r_0) = f(3) = 0$, there exists at least one root of $f'(x) = 0$ in $(r_0, 3)$. Let's call it $r_2$. So $f'(r_2) = 0$ for some $r_2 \in (r_0, 3)$.

Since $r_0 \in (1, 2)$, we have $0 < r_1 < r_0 < r_2 < 3$. This implies $r_1$ and $r_2$ are distinct roots of $f'(x) = 0$ in the interval $(0, 3)$.

Now let's evaluate $h(x) = f'(x)g(x)$ at these roots of $f'(x)$. $h(r_1) = f'(r_1)g(r_1) = 0 \times g(r_1) = 0$. $h(r_2) = f'(r_2)g(r_2) = 0 \times g(r_2) = 0$.

So we have found four points where $h(x)$ is zero: $0, r_1, r_2, 3$, where $0 < r_1 < r_2 < 3$. $h(0) = 0$, $h(r_1) = 0$, $h(r_2) = 0$, $h(3) = 0$.

Applying Rolle's Theorem to $h(x)$ on the intervals $[0, r_1]$, $[r_1, r_2]$, and $[r_2, 3]$:

• In $[0, r_1]$, since $h(0) = h(r_1) = 0$, there exists at least one root of $h'(x) = 0$ in $(0, r_1)$. Let's call it $c_1$. $c_1 \in (0, r_1)$.
• In $[r_1, r_2]$, since $h(r_1) = h(r_2) = 0$, there exists at least one root of $h'(x) = 0$ in $(r_1, r_2)$. Let's call it $c_2$. $c_2 \in (r_1, r_2)$.
• In $[r_2, 3]$, since $h(r_2) = h(3) = 0$, there exists at least one root of $h'(x) = 0$ in $(r_2, 3)$. Let's call it $c_3$. $c_3 \in (r_2, 3)$.

Since $0 < r_1 < r_2 < 3$, the intervals $(0, r_1)$, $(r_1, r_2)$, and $(r_2, 3)$ are disjoint. Therefore, the roots $c_1, c_2, c_3$ are distinct. All these three roots are in the interval $(0, 3)$, which is a subset of $(-1, 5)$. Thus, there are at least 3 roots of the equation $h'(x) = 0$ in the interval $(-1, 5)$.

This means the number of roots cannot be 2.