Question

Let $f$ be an odd function defined on the set of real numbers such that for $x \geqslant 0$, $f(x) = 3\sin x + 4\cos x$. Then $f(x)$ at $x = \dfrac{{ - 11\pi }}{6}$ is equal to
A. $\dfrac{{ - 3}}{2} - 2\sqrt 3$
B. $\dfrac{3}{2} - 2\sqrt 3$
C. $\dfrac{3}{2} + 2\sqrt 3$
D. $\dfrac{{ - 3}}{2} + 2\sqrt 3$

Answer 1

Here we use the concept of odd functions which is $f( - x) = - f(x)$ and solve for the value at given x. We break the angle in such a way that it is added or subtracted from $2\pi$.

Complete step-by-step answer:
We have $f(x) = 3\sin x + 4\cos x$
Also, we know any function is an odd function if it satisfies $f( - x) = - f(x)$.
Now we have to find the value of the function at point $x = \dfrac{{ - 11\pi }}{6}$
We have to find the value of $f(\dfrac{{ - 11\pi }}{6})$
Since, f is an odd function, therefore, we can use the concept $f( - x) = - f(x)$. Substitute $x = \dfrac{{ - 11\pi }}{6}$.
$\Rightarrow f(\dfrac{{ - 11\pi }}{6}) = - f(\dfrac{{11\pi }}{6})$
Now we can break the angle inside the function as
$\Rightarrow \dfrac{{11\pi }}{6} = \dfrac{{12\pi - \pi }}{6}$
Separating the fraction into two parts
$\Rightarrow \dfrac{{11\pi }}{6} = \dfrac{{12\pi }}{6} - \dfrac{\pi }{6}$
Cancel out common factors from numerator and denominator
$\Rightarrow \dfrac{{11\pi }}{6} = 2\pi - \dfrac{\pi }{6}$
Therefore, we can write
$f(\dfrac{{ - 11\pi }}{6}) = - f(2\pi - \dfrac{\pi }{6})$
Now we know $f(x) = 3\sin x + 4\cos x$
Put $x = 2\pi - \dfrac{\pi }{6}$
$\Rightarrow f(\dfrac{{11\pi }}{6}) = 3\sin \left( {2\pi - \dfrac{\pi }{6}} \right) + 4\cos \left( {2\pi - \dfrac{\pi }{6}} \right)$ … (1)
Now we will use the quadrant graph to convert the angles.

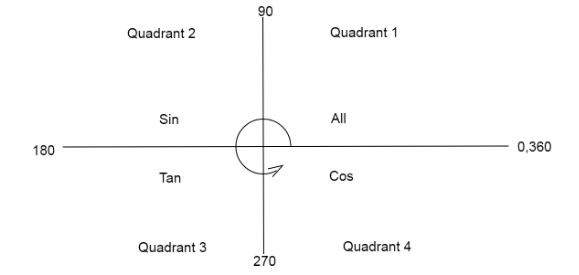
Here we denote $2\pi = {360^ \circ },\pi = {180^ \circ }$
Now we calculate the values of both the functions on RHS of the equation using the quadrant diagram.
For $\sin \left( {2\pi - \dfrac{\pi }{6}} \right)$, we are subtracting from $2\pi$which goes into the fourth quadrant where sin function is negative.
So, the value of $\sin \left( {2\pi - \dfrac{\pi }{6}} \right) = - \sin (\dfrac{\pi }{6}) = - \dfrac{1}{2}$ … (2)
For $\cos \left( {2\pi - \dfrac{\pi }{6}} \right)$, we are subtracting from $2\pi$which goes into the fourth quadrant where the cos function is positive.
So, the value of $\cos \left( {2\pi - \dfrac{\pi }{6}} \right) = \cos (\dfrac{\pi }{6}) = \dfrac{{\sqrt 3 }}{2}$ … (3)
Substitute the values from equation (2) and equation (3) in equation (1)
$\Rightarrow f(x) = 3(\dfrac{{ - 1}}{2}) + 4(\dfrac{{\sqrt 3 }}{2})$
Multiply the terms in the bracket.

$$\Rightarrow f(\dfrac{{11\pi }}{6}) = \dfrac{{ - 3}}{2} + \dfrac{{4\sqrt 3 }}{2} \\\ \Rightarrow f(\dfrac{{11\pi }}{6}) = \dfrac{{ - 3}}{2} + 2\sqrt 3 \\\$$

So now $f( - \dfrac{{11\pi }}{6}) = - f(\dfrac{{11\pi }}{6})$
Therefore,

$$\Rightarrow f( - \dfrac{{11\pi }}{6}) = - [\dfrac{{ - 3}}{2} + 2\sqrt 3 ] \\\ \Rightarrow f( - \dfrac{{11\pi }}{6}) = \dfrac{3}{2} - 2\sqrt 3 \\\$$

So, option B is correct.

Note: Students are likely to make mistakes while calculating the values from the quadrant diagram, keep in mind that we always move anti-clockwise as we add the angles, so when we subtract the angle we move backwards or clockwise to see which quadrant our function lies in.