Question

Let 'f' be an even periodic function with period '4' such that f(x) = 2x - 1, 0 ≤ x ≤ 2. The number of solutions of the equation f(x) = 1 in [-10, 20] are

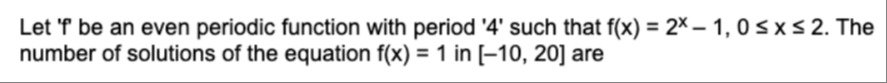
• A. 7
• B. 8
• C. 15
• D. 16

Answer 1

Answer: (C)

15

Answer 2

The function 'f' is an even periodic function with period '4', and for $0 \le x \le 2$, $f(x) = 2^x - 1$. We need to find the number of solutions for $f(x) = 1$ in the interval $[-10, 20]$.

First, let's define $f(x)$ over a full period $[0, 4]$. For $0 \le x \le 2$, $f(x) = 2^x - 1$. Since 'f' is an even function, $f(-x) = f(x)$. For $-2 \le x \le 0$, let $y = -x$, so $0 \le y \le 2$. Then $f(x) = f(-x) = f(y) = 2^y - 1 = 2^{-x} - 1$. Since 'f' is periodic with period 4, $f(x+4) = f(x)$. For $2 \le x \le 4$, $x-4$ is in $[-2, 0]$. So, $f(x) = f(x-4) = 2^{-(x-4)} - 1 = 2^{4-x} - 1$.

Thus, $f(x)$ over $[0, 4]$ is: $f(x) = \begin{cases} 2^x - 1 & 0 \le x \le 2 \\ 2^{4-x} - 1 & 2 \le x \le 4 \end{cases}$

Now, let's find the solutions for $f(x) = 1$ in the interval $[0, 4]$: For $0 \le x \le 2$: $2^x - 1 = 1 \implies 2^x = 2 \implies x = 1$. This solution is in $[0, 2]$.

For $2 \le x \le 4$: $2^{4-x} - 1 = 1 \implies 2^{4-x} = 2 \implies 4-x = 1 \implies x = 3$. This solution is in $[2, 4]$.

So, in the interval $[0, 4]$, there are two solutions: $x=1$ and $x=3$.

Due to the periodicity of 4, the general solutions are of the form $x = 1 + 4k$ and $x = 3 + 4k$, where $k$ is an integer.

Now, we need to find how many of these solutions lie in the interval $[-10, 20]$.

For solutions of the form $x = 1 + 4k$: $-10 \le 1 + 4k \le 20$ $-11 \le 4k \le 19$ $-\frac{11}{4} \le k \le \frac{19}{4}$ $-2.75 \le k \le 4.75$ The integer values for $k$ are $-2, -1, 0, 1, 2, 3, 4$. This gives $4 - (-2) + 1 = 7$ solutions.

For solutions of the form $x = 3 + 4k$: $-10 \le 3 + 4k \le 20$ $-13 \le 4k \le 17$ $-\frac{13}{4} \le k \le \frac{17}{4}$ $-3.25 \le k \le 4.25$ The integer values for $k$ are $-3, -2, -1, 0, 1, 2, 3, 4$. This gives $4 - (-3) + 1 = 8$ solutions.

The total number of distinct solutions in $[-10, 20]$ is the sum of the solutions from both forms: $7 + 8 = 15$.