Question

Let f be a real valued function defined by

$f(x) = \frac{e^{x} - e^{-|x|}}{e^{x} + e^{|x|}},$ then the range of f(x) is

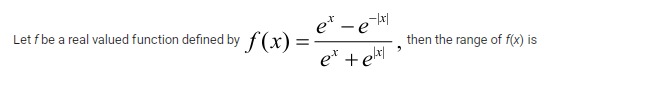
• A. $(0,1)$
• B. $[0,1)$
• C. $(-1,1)$
• D. $[0, 1/2)$

Answer 1

Answer: (D)

[0, 1/2)

Answer 2

The function is given by $f(x) = \frac{e^{x} - e^{-|x|}}{e^{x} + e^{|x|}}$. To determine the range of $f(x)$, we need to analyze the function based on the definition of $|x|$. We consider two cases: $x \ge 0$ and $x < 0$.

Case 1: $x \ge 0$

In this case, $|x| = x$. Substitute $|x|=x$ into the function:

$f(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{x}} = \frac{e^{x} - e^{-x}}{2e^{x}} = \frac{1}{2} - \frac{1}{2}e^{-2x}$

Now, let's find the range of $f(x)$ for $x \ge 0$. Since $x \ge 0$:

$2x \ge 0$

$-2x \le 0$

$e^{-2x} \le e^0$

$e^{-2x} \le 1$

Also, as $x \to \infty$, $e^{-2x} \to 0$. So, $0 < e^{-2x} \le 1$.

Now, let's build up the expression for $f(x)$:

$-\frac{1}{2}(1) \le -\frac{1}{2}e^{-2x} < -\frac{1}{2}(0)$

$-\frac{1}{2} \le -\frac{1}{2}e^{-2x} < 0$

$\frac{1}{2} - \frac{1}{2} \le \frac{1}{2} - \frac{1}{2}e^{-2x} < \frac{1}{2} + 0$

$0 \le f(x) <frac{1}{2}$

So, for $x \ge 0$, the range of $f(x)$ is $[0, \frac{1}{2})$. Note that $f(0) = \frac{1}{2} - \frac{1}{2}e^{0} = \frac{1}{2} - \frac{1}{2} = 0$, which is the lower bound.

Case 2: $x < 0$

In this case, $|x| = -x$. Substitute $|x|=-x$ into the function:

$f(x) = \frac{e^{x} - e^{-(-x)}}{e^{x} + e^{-x}} = \frac{e^{x} - e^{x}}{e^{x} + e^{-x}} = \frac{0}{e^{x} + e^{-x}}$

Since $e^x > 0$ and $e^{-x} > 0$ for all real $x$, the denominator $e^x + e^{-x}$ is always positive and never zero. Therefore, for $x < 0$, $f(x) = 0$. The range for this case is $\{0\}$.

Combining the ranges

The total range of $f(x)$ is the union of the ranges from both cases:

Range of $f(x) = \{0\} \cup [0, \frac{1}{2})$

Range of $f(x) = [0, \frac{1}{2})$