Solveeit Logo
Login

Question

Question: Let f be a function from \(f:R\to R\) defined as \(f\left( x \right)={{e}^{{{x}^{2}}}}+\cos x\) then...

Let f be a function from f:R→Rf:R\to R defined as f(x)=ex2+cos⁡xf\left( x \right)={{e}^{{{x}^{2}}}}+\cos x then f is

& \text{A}.\text{ One}-\text{one and onto} \\\ & \text{B}.\text{ One}-\text{one and into} \\\ & \text{C}.\text{ Many}-\text{one and onto} \\\ & \text{D}.\text{ Many}-\text{one and into} \\\ \end{aligned}$$
Explanation

Solution

First we will define one-one and onto function. If g:X→Yg:X\to Y is a function then g(x1)=g(x2)⇒x1=x2g\left( {{x}_{1}} \right)=g\left( {{x}_{2}} \right)\Rightarrow {{x}_{1}}={{x}_{2}} then g is one-one otherwise many-one. So, we will assume a value x,y∈Rx,y\in R such that f (y) = f (x) then check whether x = y or not. Similarly, a function is onto if every element in the domain has a preimage, so, we will check if any value of k doesn't have pre image with respect to f in k.

Complete step by step answer:
Let us define a function g:X→Yg:X\to Y such that g(x)=y ∀x∈X,y∈Yg\left( x \right)=y\text{ }\forall \text{x}\in \text{X,y}\in \text{Y}
Then function g (x) is called one-one if for g(x1)=g(x2)⇒x1=x2g\left( {{x}_{1}} \right)=g\left( {{x}_{2}} \right)\Rightarrow {{x}_{1}}={{x}_{2}} where x1,x2∈X{{x}_{1}},{{x}_{2}}\in X
If for g(x1)=g(x2)⇒x1≠x2g\left( {{x}_{1}} \right)=g\left( {{x}_{2}} \right)\Rightarrow {{x}_{1}}\ne {{x}_{2}} then g (x) is many-one function.
A function ‘g’ as defined above is called onto a function if ∀y∈Y,x∈X\forall y\in Y, x\in X such that g (x) = y.
Basically every element y∈Yy\in Y has its pre image in X∈YX\in Y
If g (x) doesn't satisfy this condition then it is called into function.
We are given f(x):R→R f(x)=ex2+cos⁡x \begin{aligned} & f\left( x \right):R\to R \\\ & f\left( x \right)={{e}^{{{x}^{2}}}}+\cos x \\\ \end{aligned}
Consider x1=π∈R and x2=−π∈R{{x}_{1}}=\pi \in R\text{ and }{{x}_{2}}=-\pi \in R
Then let us compute f(π) and f(−π)f\left( \pi \right)\text{ and }f\left( -\pi \right)
Value of f(π)=eπ2+cos⁡π . . . . . . . . (i)f\left( \pi \right)={{e}^{{{\pi }^{2}}}}+\cos \pi \text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (i)} and value of f(−π)f\left( -\pi \right) is f(−π)=e(−π)2+cos⁡(−π)f\left( -\pi \right)={{e}^{{{\left( -\pi \right)}^{2}}}}+\cos \left( -\pi \right)
Now as cos⁡(−θ)=cos⁡θ and (−π)2=π\cos \left( -\theta \right)=\cos \theta \text{ and }{{\left( -\pi \right)}^{2}}=\pi
f(−π)=eπ2+cos⁡π . . . . . . . . (ii)f\left( -\pi \right)={{e}^{{{\pi }^{2}}}}+\cos \pi \text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (ii)}
From equation (i) and (ii) we see that
f(π)=f(−π) but π≠−πf\left( \pi \right)=f\left( -\pi \right)\text{ but }\pi \ne -\pi
For π∈R and −π∈R and f(π)=f(−π)\pi \in R\text{ and }-\pi \in R\text{ and }f\left( \pi \right)=f\left( -\pi \right)
We did not get π=−π\pi =-\pi
Hence, f is not a one-one function.
Thus, f is a many-one function.
Finally we will check for onto.
f is defined from R→RR\to R which is real and has all positive and negative values. Now, consider the fact that ex≥0 ∀x∈1R{{e}^{x}}\ge 0\text{ }\forall x\in 1R
Graph of ex{{e}^{x}} is as below:

So, f(x)=ex2+cos⁡xf\left( x \right)={{e}^{{{x}^{2}}}}+\cos x
Let x=πx=\pi then as π∈R\pi \in R so f(π)f\left( \pi \right) is defined
f(π)=eπ2+cos⁡πf\left( \pi \right)={{e}^{{{\pi }^{2}}}}+\cos \pi
Now value of cos⁡π=−1\cos \pi =-1
Now as eπ2=e(3.14)2 and (3.14)2 > 1{{e}^{{{\pi }^{2}}}}={{e}^{{{\left( 3.14 \right)}^{2}}}}\text{ and }{{\left( 3.14 \right)}^{2}}\text{ }>\text{ }1
By graph of ex{{e}^{x}} we have e(3.14)2 > 1{{e}^{{{\left( 3.14 \right)}^{2}}}}\text{ }>\text{ }1
As e0=1{{e}^{0}}=1

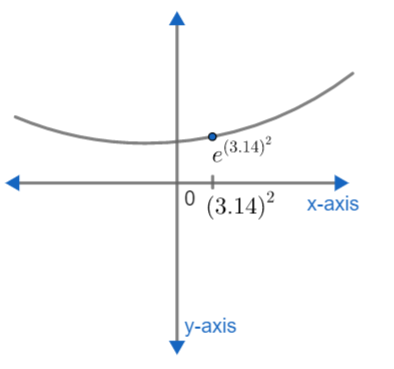
So as eπ2 > 1⇒eπ2−1 > 0{{e}^{{{\pi }^{2}}}}\text{ }>\text{ }1\Rightarrow {{e}^{{{\pi }^{2}}}}-1\text{ }>\text{ 0}
Hence, f(π) > 0f\left( \pi \right)\text{ }>\text{ }0 that is f(π)f\left( \pi \right) is positive.
As a range of cos⁡θ=[−1,1]\cos \theta =\left[ -1,1 \right] therefore, it can have no values less than -1 and greater than +1.
So, we have observed that the least value of cos⁡x=−1\cos x=-1 at x=πx=\pi is giving f(x)=f(π)f\left( x \right)=f\left( \pi \right) as positive.
Therefore, as it is giving the value of f (x) at least the value of cos x.
i) For any values of cos x, f (x) is always positive. But f was defined from R→RR\to R
ii) Negative reals are not in the image of f.
iii) There exist negative reals whose preimage is not present in f.
Therefore, f is not onto. f is into.

So, the correct answer is “Option D”.

Note: The possible confusion is the onto part. There is another way to see if the function f (x) is onto or not.
Observe that ex > 0 ∀x∈R{{e}^{x}}\text{ }>\text{ }0\text{ }\forall \text{x}\in \text{R} and cos⁡(−θ)=cos⁡θ\cos \left( -\theta \right)=\cos \theta whose value lies between [-1, 1]. So, even if cos⁡θ\cos \theta has -1 as value then also the term eπ2−1{{e}^{{{\pi }^{2}}}}-1 is positive as eπ2=e(3.14)2 > 1{{e}^{{{\pi }^{2}}}}={{e}^{{{\left( 3.14 \right)}^{2}}}}\text{ }>\text{ }1