Solveeit Logo
Login

Question

Question: Let $f$ be a function defined as $f: [-3, 3] \rightarrow [-3, 3]$ such that $f(x) = \sqrt{x^2 + 2x +...

Let ff be a function defined as f:[−3,3]→[−3,3]f: [-3, 3] \rightarrow [-3, 3] such that f(x)=x2+2x+1−x2−2x+1f(x) = \sqrt{x^2 + 2x + 1} - \sqrt{x^2 - 2x + 1}. Then

A

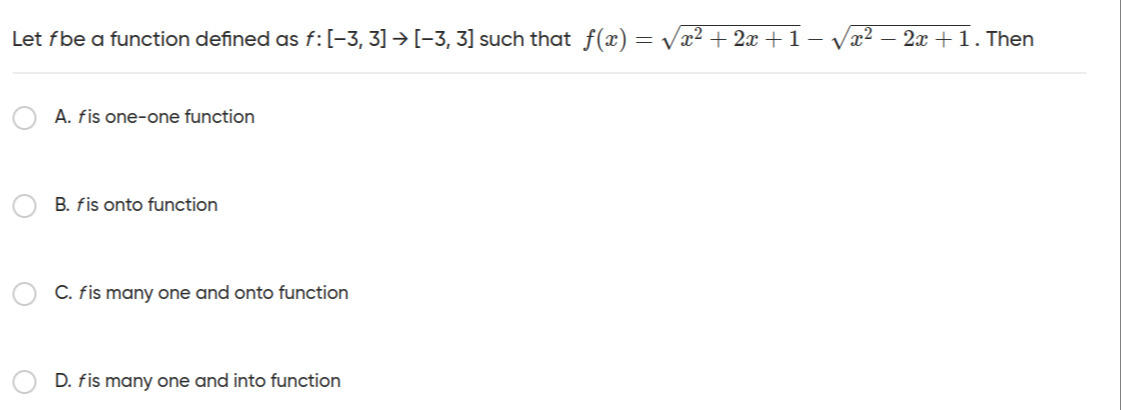
ff is one-one function

B

ff is onto function

C

ff is many one and onto function

D

ff is many one and into function

Answer

D. ff is many one and into function

Explanation

Solution

The given function is f:[−3,3]→[−3,3]f: [-3, 3] \rightarrow [-3, 3] defined as f(x)=x2+2x+1−x2−2x+1f(x) = \sqrt{x^2 + 2x + 1} - \sqrt{x^2 - 2x + 1}.

1. Simplify the function: We can simplify the terms under the square root: x2+2x+1=(x+1)2x^2 + 2x + 1 = (x+1)^2 x2−2x+1=(x−1)2x^2 - 2x + 1 = (x-1)^2

So, f(x)=(x+1)2−(x−1)2f(x) = \sqrt{(x+1)^2} - \sqrt{(x-1)^2}. Using the property a2=∣a∣\sqrt{a^2} = |a|, we get: f(x)=∣x+1∣−∣x−1∣f(x) = |x+1| - |x-1|

2. Define the function piecewise: The critical points for the absolute values are x=−1x = -1 and x=1x = 1. We analyze the function in intervals based on these points within the domain [−3,3][-3, 3].

  • Case 1: For −3≤x<−1-3 \le x < -1
    In this interval, x+1<0x+1 < 0 and x−1<0x-1 < 0.
    So, ∣x+1∣=−(x+1)|x+1| = -(x+1) and ∣x−1∣=−(x−1)|x-1| = -(x-1).
    f(x)=−(x+1)−(−(x−1))f(x) = -(x+1) - (-(x-1))
    f(x)=−x−1+x−1f(x) = -x - 1 + x - 1
    f(x)=−2f(x) = -2

  • Case 2: For −1≤x<1-1 \le x < 1
    In this interval, x+1≥0x+1 \ge 0 and x−1<0x-1 < 0.
    So, ∣x+1∣=x+1|x+1| = x+1 and ∣x−1∣=−(x−1)|x-1| = -(x-1).
    f(x)=(x+1)−(−(x−1))f(x) = (x+1) - (-(x-1))
    f(x)=x+1+x−1f(x) = x+1 + x-1
    f(x)=2xf(x) = 2x

  • Case 3: For 1≤x≤31 \le x \le 3
    In this interval, x+1>0x+1 > 0 and x−1≥0x-1 \ge 0.
    So, ∣x+1∣=x+1|x+1| = x+1 and ∣x−1∣=x−1|x-1| = x-1.
    f(x)=(x+1)−(x−1)f(x) = (x+1) - (x-1)
    f(x)=x+1−x+1f(x) = x+1 - x+1
    f(x)=2f(x) = 2

Combining these cases, the function f(x)f(x) is: f(x)={−2if −3≤x<−12xif −1≤x<12if 1≤x≤3f(x) = \begin{cases} -2 & \text{if } -3 \le x < -1 \\ 2x & \text{if } -1 \le x < 1 \\ 2 & \text{if } 1 \le x \le 3 \end{cases}

3. Determine if ff is one-one or many-one: A function is one-one if distinct elements in the domain map to distinct elements in the codomain. Otherwise, it's many-one.
From the piecewise definition:

  • For x∈[−3,−1)x \in [-3, -1), f(x)=−2f(x) = -2. For example, f(−3)=−2f(-3) = -2 and f(−2)=−2f(-2) = -2. Since −3≠−2-3 \ne -2 but f(−3)=f(−2)f(-3) = f(-2), the function is many-one.
  • Similarly, for x∈[1,3]x \in [1, 3], f(x)=2f(x) = 2. For example, f(1)=2f(1) = 2 and f(2)=2f(2) = 2. Since 1≠21 \ne 2 but f(1)=f(2)f(1) = f(2), the function is many-one.

Thus, ff is a many-one function.

4. Determine the range of ff:

  • For −3≤x<−1-3 \le x < -1, the range is {−2}\{-2\}.
  • For −1≤x<1-1 \le x < 1, f(x)=2xf(x) = 2x. As xx varies from −1-1 (inclusive) to 11 (exclusive), f(x)f(x) varies from 2(−1)=−22(-1) = -2 to 2(1)=22(1) = 2 (exclusive). So, the range for this part is [−2,2)[-2, 2).
  • For 1≤x≤31 \le x \le 3, the range is {2}\{2\}.

Combining these, the overall range of ff is {−2}∪[−2,2)∪{2}=[−2,2]\{-2\} \cup [-2, 2) \cup \{2\} = [-2, 2].

5. Determine if ff is onto or into: The codomain of the function is given as [−3,3][-3, 3].
The range of the function is [−2,2][-2, 2].
Since the range [−2,2][-2, 2] is a proper subset of the codomain [−3,3][-3, 3] (i.e., Range ≠\ne Codomain), the function is into.

Conclusion: The function ff is many-one and into.