Solveeit Logo
Login

Question

Question: Let f be a continuous function satisfying the equation $\int_{0}^{x} f(t) dt + \int_{0}^{x} tf(x-t)d...

Let f be a continuous function satisfying the equation ∫0xf(t)dt+∫0xtf(x−t)dt=e−x−1\int_{0}^{x} f(t) dt + \int_{0}^{x} tf(x-t)dt = e^{-x}-1, then find the value of e10f(10)e^{10}f(10).

A

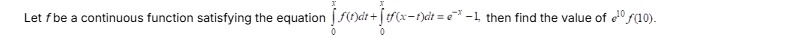
9

B

e^10

C

10

D

e^-10

Answer

9

Explanation

Solution

The given equation is: ∫0xf(t)dt+∫0xtf(x−t)dt=e−x−1\int_{0}^{x} f(t) dt + \int_{0}^{x} tf(x-t)dt = e^{-x}-1 We can solve this integral equation using Laplace Transforms. Let F(s)=L{f(t)}(s)F(s) = \mathcal{L}\{f(t)\}(s) be the Laplace transform of f(t)f(t).

The Laplace transform of the first term is: L{∫0xf(t)dt}(s)=F(s)s\mathcal{L}\left\{\int_{0}^{x} f(t) dt\right\}(s) = \frac{F(s)}{s} This is because ∫0xf(t)dt\int_{0}^{x} f(t) dt is the convolution of the function f(t)f(t) with the constant function 11. L{1}(s)=1/s\mathcal{L}\{1\}(s) = 1/s.

The second term is a convolution integral: ∫0xtf(x−t)dt\int_{0}^{x} tf(x-t)dt. This is the convolution of g(t)=tg(t)=t and f(t)f(t), denoted as (g∗f)(x)(g*f)(x). The Laplace transform of g(t)=tg(t)=t is L{t}(s)=1s2\mathcal{L}\{t\}(s) = \frac{1}{s^2}. So, the Laplace transform of the second term is: L{∫0xtf(x−t)dt}(s)=L{t}(s)L{f(t)}(s)=1s2F(s)\mathcal{L}\left\{\int_{0}^{x} tf(x-t)dt\right\}(s) = \mathcal{L}\{t\}(s) \mathcal{L}\{f(t)\}(s) = \frac{1}{s^2} F(s)

The Laplace transform of the right-hand side is: L{e−x−1}(s)=L{e−x}(s)−L{1}(s)=1s+1−1s\mathcal{L}\{e^{-x}-1\}(s) = \mathcal{L}\{e^{-x}\}(s) - \mathcal{L}\{1\}(s) = \frac{1}{s+1} - \frac{1}{s} L{e−x−1}(s)=s−(s+1)s(s+1)=−1s(s+1)\mathcal{L}\{e^{-x}-1\}(s) = \frac{s - (s+1)}{s(s+1)} = \frac{-1}{s(s+1)}

Now, we equate the Laplace transforms of both sides of the given equation: F(s)s+F(s)s2=−1s(s+1)\frac{F(s)}{s} + \frac{F(s)}{s^2} = \frac{-1}{s(s+1)} To solve for F(s)F(s), we can multiply the entire equation by s2s^2: sF(s)+F(s)=−s2s(s+1)sF(s) + F(s) = \frac{-s^2}{s(s+1)} F(s)(s+1)=−ss+1F(s)(s+1) = \frac{-s}{s+1} F(s)=−s(s+1)2F(s) = \frac{-s}{(s+1)^2}

To find f(x)f(x), we need to compute the inverse Laplace transform of F(s)F(s). We can rewrite F(s)F(s) as: F(s)=−s(s+1)2=−(s+1)+1(s+1)2=−(s+1)(s+1)2+1(s+1)2F(s) = \frac{-s}{(s+1)^2} = \frac{-(s+1)+1}{(s+1)^2} = \frac{-(s+1)}{(s+1)^2} + \frac{1}{(s+1)^2} F(s)=−1s+1+1(s+1)2F(s) = \frac{-1}{s+1} + \frac{1}{(s+1)^2}

Now, we find the inverse Laplace transform of each term: L−1{1s+a}(x)=e−ax\mathcal{L}^{-1}\left\{\frac{1}{s+a}\right\}(x) = e^{-ax} L−1{1(s+a)2}(x)=xe−ax\mathcal{L}^{-1}\left\{\frac{1}{(s+a)^2}\right\}(x) = xe^{-ax} Using these formulas with a=1a=1: L−1{−1s+1}(x)=−e−x\mathcal{L}^{-1}\left\{\frac{-1}{s+1}\right\}(x) = -e^{-x} L−1{1(s+1)2}(x)=xe−x\mathcal{L}^{-1}\left\{\frac{1}{(s+1)^2}\right\}(x) = xe^{-x} Therefore, the function f(x)f(x) is: f(x)=−e−x+xe−x=e−x(x−1)f(x) = -e^{-x} + xe^{-x} = e^{-x}(x-1)

The problem asks for the value of e10f(10)e^{10}f(10). First, we find f(10)f(10): f(10)=e−10(10−1)=9e−10f(10) = e^{-10}(10-1) = 9e^{-10} Now, we calculate e10f(10)e^{10}f(10): e10f(10)=e10⋅(9e−10)=9e^{10}f(10) = e^{10} \cdot (9e^{-10}) = 9