Question

Let $f$ be a continuous and differentiable function in $(k_1, k_2)$. If $f(x) \cdot f'(x) \geq x\sqrt{1-(f(x))^4}$ and $\lim_{x \to k_1^{+}} (f(x))^2 = 1$ & $\lim_{x \to k_2^{-}} (f(x))^2 = \frac{1}{2}$. Then minimum value of $[\frac{k_1^2}{4} - k_2^2]$ is where $[.]$ represents greatest integer function.

Answer 1

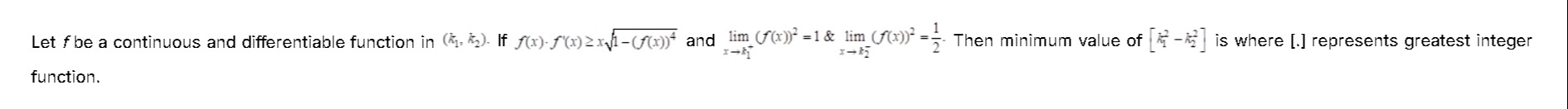
0

Answer 2

We start with

$$f(x)f'(x)\ge x\sqrt{1-\bigl(f(x)^4\bigr)},$$

which we rewrite by noting that

$$\frac{d}{dx}\Bigl(f(x)^2\Bigr)=2f(x)f'(x).$$

Thus

$$\frac{1}{2}\frac{d}{dx}\Bigl(f(x)^2\Bigr)\ge x\sqrt{1-\bigl(f(x)^4\bigr)}.$$

Introduce the substitution

$$u(x)=f(x)^2\quad\text{so that}\quad f(x)^4=u(x)^2.$$

Then

$$\frac{du}{dx}\ge 2x\sqrt{1-u^2}.$$

Now, integrate from $x=k_1$ to $x=k_2$. The given limits are

$$u(k_1)=\lim_{x\to k_1^+}f(x)^2=1,\quad u(k_2)=\lim_{x\to k_2^-}f(x)^2=\frac12.$$

Integrate the inequality in the “equality‐case” (which gives the best possibility for “optimizing” the endpoints)

$$\int_{u=1}^{1/2}\frac{du}{\sqrt{1-u^2}}=\int_{x=k_1}^{k_2}2x\,dx.$$

The left‐side is computed as

$$\int_{1}^{1/2}\frac{du}{\sqrt{1-u^2}} = \arcsin(u)\Big|_{1}^{1/2} = \arcsin\Bigl(\frac{1}{2}\Bigr)-\arcsin(1) =\frac{\pi}{6}-\frac{\pi}{2}=-\frac{\pi}{3}.$$

The right‐side is

$$\int_{k_1}^{k_2}2x\,dx=x^2\Big|_{k_1}^{k_2}=k_2^2-k_1^2.$$

Thus we have

$$-\frac{\pi}{3}\ge k_2^2-k_1^2\quad\Longrightarrow\quad k_1^2-k_2^2\ge\frac{\pi}{3}.$$

Now, our expression of interest is

$$A=\frac{k_1^2}{4}-k_2^2.$$

Write $k_1^2=k_2^2+\Delta$ where $\Delta\ge \frac{\pi}{3}$. Then

$$A=\frac{k_2^2+\Delta}{4}-k_2^2=\frac{\Delta}{4}-\frac{3k_2^2}{4}.$$

To maximize (i.e. “minimize the loss” in the greatest‐integer sense) this quantity we choose the smallest allowed $\Delta=\frac{\pi}{3}$ and try to make $k_2^2$ as small as possible. Clearly we may take

$$k_2^2=0,$$

which (with $k_1^2=\frac{\pi}{3}$) is admissible if one chooses the interval as $(k_1,k_2)=\Bigl(-\sqrt{\frac{\pi}{3}},\,0\Bigr)$.

In that case the value becomes

$$A=\frac{\pi/3}{4}-0=\frac{\pi}{12}\approx 0.2618.$$

Since the floor function $[\,\cdot\,]$ (greatest integer function) takes the greatest integer less than or equal to its argument, we have

$$\left[\frac{k_1^2}{4}-k_2^2\right]=\left[\frac{\pi}{12}\right]=0.$$