Question
Question: Let current i = 2 A be flowing in each part of a wire frame as shown in fig. The frame is a combinat...
Let current i = 2 A be flowing in each part of a wire frame as shown in fig. The frame is a combination of two equilateral triangles ACD and CDE of side 1 m. It is placed in uniform magnetic field B = 4 T acting perpendicular to the plane of frame. The magnitude of magnetic force acting on the frame is?
1. 24 N
2. 0 N
3. 16 N
4. 8 N
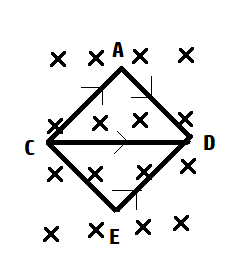
Solution
The figure shows a metallic frame of a conductor in a magnetic field directed into the page. The current is flowing in the conductor and the direction of current is shown by the arrows. The frame can be divided into two triangles- upper half and lower half. We can use the concept of a current conductor placed in a magnetic field.
Complete step by step answer:
The applied magnetic field is directed perpendicular to the plane of the frame, it will make an angle (900 ) with each edge of the conductor. We know force on a current carrying conductor is given by,
F=i(l×B) ⟹F=ilBsin90 ⟹F=ilb
Given length of each edge is 1 m and the value of current in each edge is 2 A. Hence, the force on each edge comes out to be F=ilB=2×4=N
The point to keep is that the direction of magnetic force will be the cross product of length and the field. Fleming’s left-hand rule is used here to find out the direction of force on each edge. The arrow represents the force on each edge in the figure below:
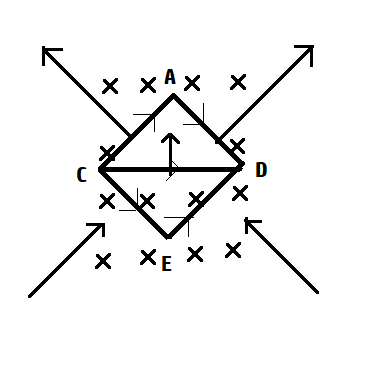
The forces on edge AC and AD are inclined at 1200, so their resultant will be calculated using parallelogram law,
