Question

Let $\cos (\alpha + \beta ) =$ $\dfrac{4}{5}$ and let $\sin (\alpha - \beta ) =$ $\dfrac{5}{{13}}$ , where 0 ≤ α, β ≤ $\dfrac{\pi }{4}$ , then $\tan 2\alpha$ is equal to
A. $\dfrac{{20}}{7}$
B. $\dfrac{{25}}{{16}}$
C. $\dfrac{{56}}{{33}}$
D. $\dfrac{{19}}{{12}}$

Answer 1

Hint : We know the cosine of any angle is the ratio of the base to hypotenuse in a right angled triangle. Similarly, sine of any angle is the ratio of the opposite side to hypotenuse in a right angled triangle. Further, we will use Pythagoras theorem to calculate the other trigonometry ratio which is $\tan 2\alpha$ .
Formula Used: The following formula is used to get to the final answer,
$\tan (\alpha + \beta ) =$ $\dfrac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \tan \beta }}$

Complete step-by-step answer :
According to the given information, we have
The first function is $\cos (\alpha + \beta ) =$ $\dfrac{4}{5}$

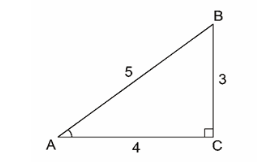
Also, we know $\cos (\alpha + \beta ) = \dfrac{4}{5}$
Therefore take the base to be 4k and hypotenuse as 5k, where k is a constant.
Further, perpendicular = $\sqrt {{{(hypotenuse)}^2}\;-{\text{ }}{{\left( {base} \right)}^2}}$
$\Rightarrow \sqrt {{{(5k)}^2} - {{(4k)}^2}}$ $= \sqrt {9{k^2}}$
Finally we get the perpendicular to be 3k.
Now for a right angled triangle ABC we know that,
$\tan (\alpha + \beta ) =$ $\dfrac{3}{4}$ $...(1)$
The second function is $\sin (\alpha - \beta ) =$ $\dfrac{5}{{13}}$

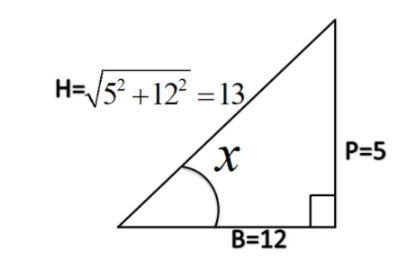
Also, we know $\sin (\alpha - \beta ) = \dfrac{5}{{13}}$
Therefore, take the perpendicular to be 5k and hypotenuse as 13k, where k is a constant.
Further, base = $\sqrt {{{(hypotenuse)}^2}\;-{\text{ }}{{\left( {perpendicular} \right)}^2}}$
$\Rightarrow \sqrt {{{(13k)}^2} - {{(5k)}^2}}$ $= \sqrt {144{k^2}}$
Finally we get the base to be 12k.
Now for a right angled triangle ABC we know that,
Hence we get,
$\tan (\alpha - \beta ) =$ $\dfrac{5}{{12}}$ $...(2)$
According to the given data,
The following formula is used to get,
$\tan (\alpha + \beta ) =$ $\dfrac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \tan \beta }}$
$\tan ((\alpha + \beta ) + (\alpha - \beta ))$ = $\dfrac{{\tan (\alpha + \beta ) + \tan (\alpha - \beta )}}{{1 - \tan (\alpha + \beta )\tan (\alpha - \beta )}}$
On simplifying further we get,
$\tan 2\alpha$ $= \dfrac{{\dfrac{3}{4} + \dfrac{5}{{12}}}}{{1 - \dfrac{3}{4} \times \dfrac{5}{{12}}}}$
$\Rightarrow \dfrac{{\dfrac{{36 + 20}}{{48}}}}{{\dfrac{{48 - 15}}{{48}}}}$ $= \dfrac{{56}}{{33}}$
So, the correct answer is “$\dfrac{{56}}{{33}}$ ”.

Note : In order to solve problems of this type the key is to have a basic understanding of trigonometric equations and values and also learn its implications. Students should be aware of applications of the trigonometric values in order to simplify the given equation.