Question

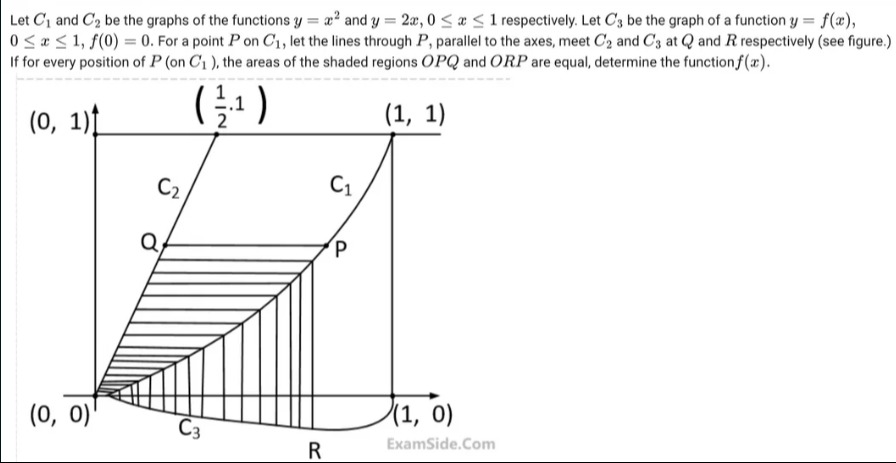
Let $C_1$ and $C_2$ be the graphs of the functions $y=x^2$ and $y=2x$, $0 \leq x \leq 1$ respectively. Let $C_3$ be the graph of a function $y=f(x)$, $0 \leq x \leq 1$, $f(0)=0$. For a point $P$ on $C_1$, let the lines through $P$, parallel to the axes, meet $C_2$ and $C_3$ at $Q$ and $R$ respectively (see figure.)

If for every position of $P$ (on $C_1$), the areas of the shaded regions $OPQ$ and $ORP$ are equal, determine the function $f(x)$.

Answer 1

f(x)=\frac{x^3}{2}

Answer 2

We start by letting

$$P=(a,a^2) \quad (0\le a\le 1)$$

since $P$ lies on $C_1: y=x^2$.

Step 1. Finding $Q$:

The horizontal line through $P$ has equation

$$y=a^2.$$

This line meets $C_2: y=2x$ when

$$a^2=2x\quad\Longrightarrow\quad x=\frac{a^2}{2}.$$

Thus,

$$Q=\left(\frac{a^2}{2},\,a^2\right).$$

Step 2. Finding $R$:

The vertical line through $P$ is $x=a$. It meets $C_3: y=f(x)$ at

$$R=(a,f(a)).$$

We are given $f(0)=0$.

Step 3. Area Calculation:

The two shaded regions are triangles:

• $\triangle OPQ$ with vertices $O=(0,0)$, $P=(a,a^2)$, $Q=\left(\frac{a^2}{2}, a^2\right)$.
• $\triangle ORP$ with vertices $O=(0,0)$, $R=(a,f(a))$, $P=(a,a^2)$.

Using the determinant formula for the area of a triangle with vertices $(x_1,y_1)$ and $(x_2,y_2)$,

$$\text{Area}=\frac{1}{2}\left| x_1y_2-y_1x_2 \right|,$$

we find:

For $\triangle OPQ$:

$$\text{Area}_{OPQ}=\frac{1}{2}\left|a\cdot a^2-\;a^2\cdot\frac{a^2}{2}\right| =\frac{1}{2}\left(a^3-\frac{a^4}{2}\right) =\frac{a^3}{2}-\frac{a^4}{4}.$$

For $\triangle ORP$:

$$\text{Area}_{ORP}=\frac{1}{2}\left|a\cdot f(a)-a^2\cdot a\right| =\frac{1}{2}\left|a f(a)-a^3\right|.$$

Since the figure suggests that $f(a) < a^2$ (so that the vertical segment $PR$ is downward), we have:

$$|a f(a)-a^3|=a(a^2-f(a)).$$

Thus,

$$\text{Area}_{ORP}=\frac{a}{2}\left(a^2-f(a)\right).$$

Step 4. Equating the Areas:

The condition states:

$$\text{Area}_{OPQ}=\text{Area}_{ORP}.$$

Thus,

$$\frac{a^3}{2}-\frac{a^4}{4}=\frac{a}{2}(a^2-f(a)).$$

Multiply both sides by 2:

$$a^3 - \frac{a^4}{2} = a(a^2-f(a))=a^3- a f(a).$$

Subtract $a^3$ from both sides:

$$-\frac{a^4}{2}=-a f(a).$$

Multiply both sides by $-1$:

$$\frac{a^4}{2}=a f(a).$$

For $a\ne0$, dividing both sides by $a$:

$$f(a)=\frac{a^3}{2}.$$

Since $a$ was any value in $[0,1]$, we have:

$$f(x)=\frac{x^3}{2}\quad \text{for}\quad 0\le x\le 1.$$