Question

Let $C$ be the circle with centre $(0,\ 0)$ and radius $3\ units$. The equation of the locus of the mid points of the chord which subtend an angle of $\dfrac{2\pi}{3}$ at its centre .

Answer 1

In the question, we need to find the equation of the locus of the midpoint of the chord. Also given the angle at its centre. By using the property of the circle and distance formula we can find the equation of the locus of the midpoint of the chord.
Formula used :
The equation of the circle is $x^{2} + y^{2} = r^{2}$
The distance formula of the circle is
$\left( x – h \right)^{2} + \left( y – k \right)^{2} = \ r^{2}$
Where$\ (h\ ,\ k)$ is the centre point of the circle
${\ r\ }$ is the radius of the circle.

Complete answer:

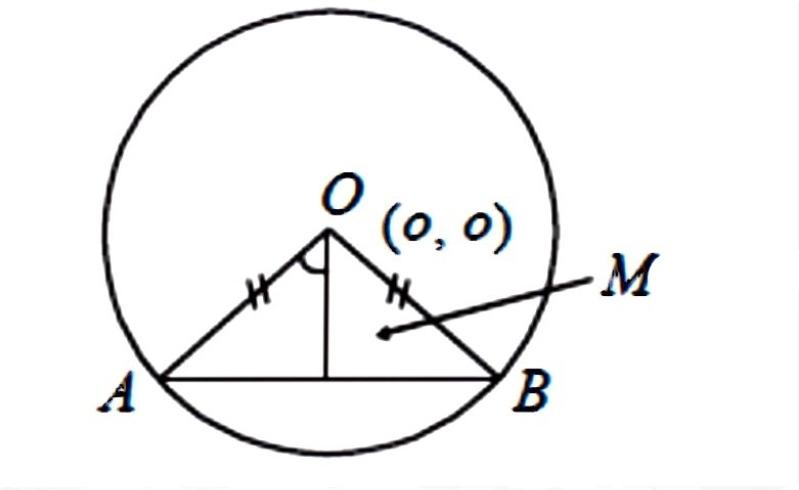
Let us assume a circle $C$with centre $O$. Let AB be the chord of the circle and $M(x, y)$ be the midpoint of AB.
Given,
$\angle\ AOM = 60$
Also given, $OA = OB = 3$
By the property of the circle,
${OM}\bot{AB}$
Now,
W. K. T :
$\cos\theta = \dfrac{{adjacent\ side}}{{hypotenuse}}$
$cos60° = \dfrac{{OM}}{{OA}}$
$\dfrac{1}{2} = \dfrac{{OM}}{3}$
By cross multiplying,
We get,
$OM = \dfrac{3}{2}$
By the distance formula,
$OM = \sqrt{x^{2} + y^{2}}$
By substituting the value,
We get,
$\dfrac{3}{2} = \sqrt{x^{2} + y^{2}}$
Squaring on both sides,
We get,
$\dfrac{9}{4} = x^{2} + y^{2}$
By rearranging the terms,
We get,
$x^{2} + y^{2} = \dfrac{9}{4}$
Thus the equation of the locus of the mid point of the chord is $x^{2} + y^{2} = \dfrac{9}{4}$
Final answer :
The equation of the locus of the mid point of the chord is $x^{2} + y^{2} = \dfrac{9}{4}$.

Note:
If the radius of different circles are equal, the circles are said to be congruent. The diameter of the circle is known as the longest chord of the circle. The radius of the circle is perpendicular to the chord bisecting the circle.