Question

Let

$\begin{vmatrix} 1+x & x & x^2 \\ x & 1+x & x^2 \\ x^2 & x & 1+x \end{vmatrix}$

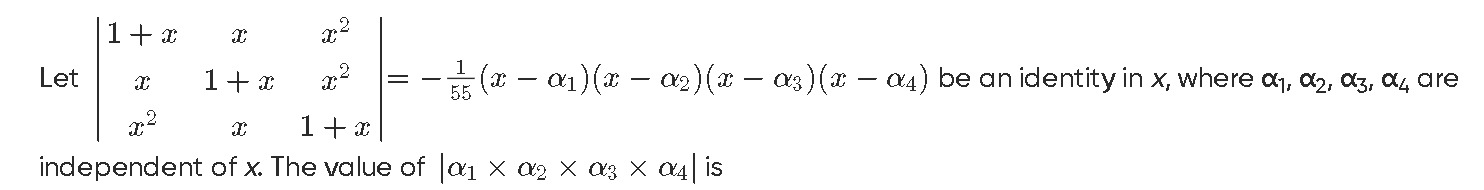
= $-\frac{1}{55}(x-\alpha_1)(x-\alpha_2)(x-\alpha_3)(x-\alpha_4)$ be an identity in $x$, where $\alpha_1$, $\alpha_2$, $\alpha_3$, $\alpha_4$ are independent of $x$. The value of $|\alpha_1 \times \alpha_2 \times \alpha_3 \times \alpha_4|$ is

Answer 1

1

Answer 2

Let the given determinant be $D(x)$.

$D(x) = \begin{vmatrix} 1+x & x & x^2 \\ x & 1+x & x^2 \\ x^2 & x & 1+x \end{vmatrix}$

To evaluate the determinant, we apply column operations: $C_1 \to C_1 + C_2 + C_3$ $D(x) = \begin{vmatrix} (1+x)+x+x^2 & x & x^2 \\ x+(1+x)+x^2 & 1+x & x^2 \\ x^2+x+(1+x) & x & 1+x \end{vmatrix}$ $D(x) = \begin{vmatrix} 1+2x+x^2 & x & x^2 \\ 1+2x+x^2 & 1+x & x^2 \\ 1+2x+x^2 & x & 1+x \end{vmatrix}$

Factor out $(1+2x+x^2)$ from the first column. Note that $1+2x+x^2 = (1+x)^2$. $D(x) = (1+x)^2 \begin{vmatrix} 1 & x & x^2 \\ 1 & 1+x & x^2 \\ 1 & x & 1+x \end{vmatrix}$

Now, apply row operations to simplify further: $R_2 \to R_2 - R_1$ $R_3 \to R_3 - R_1$ $D(x) = (1+x)^2 \begin{vmatrix} 1 & x & x^2 \\ 0 & (1+x)-x & x^2-x^2 \\ 0 & x-x & (1+x)-x^2 \end{vmatrix}$ $D(x) = (1+x)^2 \begin{vmatrix} 1 & x & x^2 \\ 0 & 1 & 0 \\ 0 & 0 & 1+x-x^2 \end{vmatrix}$

This is an upper triangular matrix (or rather, its determinant can be easily evaluated by expanding along the first column). $D(x) = (1+x)^2 \cdot 1 \cdot \begin{vmatrix} 1 & 0 \\ 0 & 1+x-x^2 \end{vmatrix}$ $D(x) = (1+x)^2 (1 \cdot (1+x-x^2) - 0 \cdot 0)$ $D(x) = (1+x)^2 (1+x-x^2)$

Expand the expression: $D(x) = (1+2x+x^2)(1+x-x^2)$ $D(x) = 1(1+x-x^2) + 2x(1+x-x^2) + x^2(1+x-x^2)$ $D(x) = (1+x-x^2) + (2x+2x^2-2x^3) + (x^2+x^3-x^4)$

Combine like terms: $D(x) = -x^4 + (-2x^3+x^3) + (-x^2+2x^2+x^2) + (x+2x) + 1$ $D(x) = -x^4 - x^3 + 2x^2 + 3x + 1$

We are given that $D(x) = -\frac{1}{55}(x-\alpha_1)(x-\alpha_2)(x-\alpha_3)(x-\alpha_4)$. Let $P(x) = (x-\alpha_1)(x-\alpha_2)(x-\alpha_3)(x-\alpha_4)$. Then $D(x) = -\frac{1}{55} P(x)$. This implies $P(x) = -55 D(x)$. Substitute the expression for $D(x)$: $P(x) = -55 (-x^4 - x^3 + 2x^2 + 3x + 1)$ $P(x) = 55x^4 + 55x^3 - 110x^2 - 165x - 55$

The polynomial $P(x)$ has roots $\alpha_1, \alpha_2, \alpha_3, \alpha_4$. For a polynomial $a_n x^n + a_{n-1} x^{n-1} + \dots + a_1 x + a_0 = 0$, the product of the roots is given by $(-1)^n \frac{a_0}{a_n}$. In our case, $n=4$. The polynomial is $55x^4 + 55x^3 - 110x^2 - 165x - 55 = 0$. Here, $a_4 = 55$ (the coefficient of $x^4$) and $a_0 = -55$ (the constant term). The product of the roots $\alpha_1\alpha_2\alpha_3\alpha_4$ is: $\alpha_1\alpha_2\alpha_3\alpha_4 = (-1)^4 \frac{a_0}{a_4} = (1) \frac{-55}{55} = -1$.

We need to find the value of $|\alpha_1 \times \alpha_2 \times \alpha_3 \times \alpha_4|$. $|\alpha_1 \times \alpha_2 \times \alpha_3 \times \alpha_4| = |-1| = 1$.