Question

Let $\bar{p}=3ax^2\hat{i}-2(x-1)\hat{j}$, $\bar{q}=b(x-1)\hat{i}+x\hat{j}$ and $ab<0$. Then $\bar{p}$ and $\bar{q}$ are parallel for:

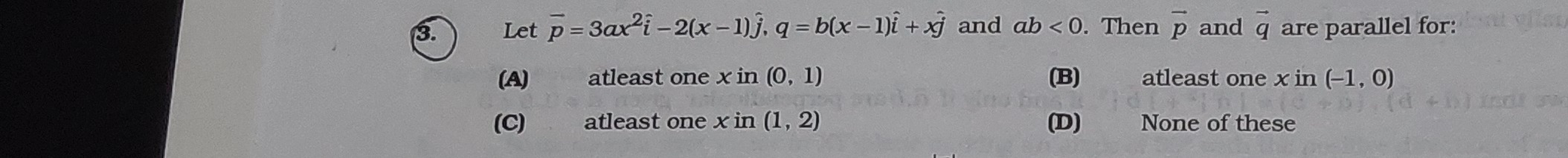
• A. atleast one x in (0, 1)
• B. atleast one x in (-1, 0)
• C. atleast one x in (1, 2)
• D. None of these

Answer 1

Answer: (A)

atleast one x in (0, 1)

Answer 2

For the vectors $\bar{p}=3ax^2\hat{i}-2(x-1)\hat{j}$ and $\bar{q}=b(x-1)\hat{i}+x\hat{j}$ to be parallel, their corresponding components must be proportional. This means: $\frac{3ax^2}{b(x-1)} = \frac{-2(x-1)}{x}$

First, we must ensure the denominators are not zero.

If $x=1$, $\bar{p}=3a\hat{i}$ and $\bar{q}=\hat{j}$. These are not parallel as $a \neq 0$ (because $ab<0$). If $x=0$, $\bar{p}=2\hat{j}$ and $\bar{q}=-b\hat{i}$. These are not parallel as $b \neq 0$ (because $ab<0$). So, $x \neq 0$ and $x \neq 1$.

Now, we can cross-multiply: $3ax^2(x) = -2(x-1)b(x-1)$ $3ax^3 = -2b(x-1)^2$ $3ax^3 = -2b(x^2 - 2x + 1)$ $3ax^3 = -2bx^2 + 4bx - 2b$

Rearrange the terms to form a cubic equation: $3ax^3 + 2bx^2 - 4bx + 2b = 0$

Given that $ab < 0$, $a$ and $b$ have opposite signs. Also, $b \neq 0$. We can divide the entire equation by $b$: $\frac{3a}{b}x^3 + 2x^2 - 4x + 2 = 0$

Let $k = \frac{a}{b}$. Since $a$ and $b$ have opposite signs, $k$ must be negative, i.e., $k < 0$. The equation becomes: $3kx^3 + 2x^2 - 4x + 2 = 0$

Let $f(x) = 3kx^3 + 2x^2 - 4x + 2$. We are looking for roots of $f(x)=0$. Since $k < 0$, let $k = -c$ where $c > 0$. Substituting $k=-c$ into the equation: $-3cx^3 + 2x^2 - 4x + 2 = 0$

Multiply by -1 to make the leading coefficient positive (optional, but can make analysis slightly cleaner): $3cx^3 - 2x^2 + 4x - 2 = 0$

Let $g(x) = 3cx^3 - 2x^2 + 4x - 2$. We need to find if $g(x)=0$ has a root in the given intervals.

We will use the Intermediate Value Theorem (IVT). $g(x)$ is a polynomial, so it is continuous everywhere.

Let's check option (A): "atleast one x in (0, 1)" Evaluate $g(x)$ at the endpoints of the interval (0, 1): $g(0) = 3c(0)^3 - 2(0)^2 + 4(0) - 2 = -2$ $g(1) = 3c(1)^3 - 2(1)^2 + 4(1) - 2 = 3c - 2 + 4 - 2 = 3c$

Since $c > 0$, we have $g(0) = -2 < 0$ and $g(1) = 3c > 0$. Because $g(0)$ and $g(1)$ have opposite signs, by the Intermediate Value Theorem, there must be at least one root $x \in (0, 1)$ such that $g(x) = 0$. Therefore, option (A) is correct.